题目内容
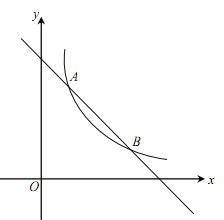
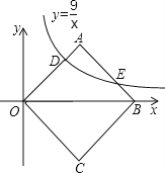
【题目】如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.
(x>0)与OA边交于点D、与AB边交于点E.
(1)求点D的坐标;
(2)求证:四边形ABCD是正方形;
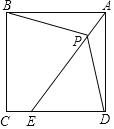
(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.
【答案】(1)点D的坐标为(3,3);(2)见解析;(3)![]() .
.
【解析】
(1)由OA=AB,∠OAB=90°可得出∠AOB=∠ABO=45°,进而可设点D的坐标为(a,a),再利用反比例函数图象上点的坐标特征结合点D在第一象限,即可求出点D的坐标;
(2)由点A与点C关于x轴对称结合OA=AB可得出OA=OC=AB=BC,进而可得出四边形ABCO是菱形,再结合∠OAB=90°,即可证出四边形ABCO是正方形;
(3)依照题意画出图形,易证△AFG≌△AEG,进而可得出S四边形OHGF=S△AOH-S△AFG=S△AOH-S△AEG,设点A的坐标为(m,m),点E的坐标为(n,![]() ),易证AG=GE,进而可得出2m-n=
),易证AG=GE,进而可得出2m-n=![]() ,再利用三角形的面积公式结合S四边形OHGF=S△AOH-S△AEG,即可求出四边形OHGF的面积.
,再利用三角形的面积公式结合S四边形OHGF=S△AOH-S△AEG,即可求出四边形OHGF的面积.
解:(1)∵OA=AB,∠OAB=90°,
∴∠AOB=∠ABO=45°,
∴设点D的坐标为(a,a).
∵点D在反比例函数y=![]() 的图象上,
的图象上,
∴a=![]() ,解得:a=±3.
,解得:a=±3.
∵点D在第一象限,
∴a=3,
∴点D的坐标为(3,3).
(2)证明:∵点A与点C关于x轴对称,
∴OA=OC,AB=BC.
又∵OA=AB,
∴OA=OC=AB=BC,
∴四边形ABCO是菱形.
又∵∠OAB=90°,
∴四边形ABCO是正方形.
(3)依照题意,画出图形,如图所示.
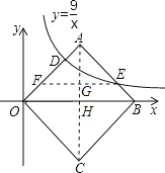
∵EG⊥AC,
∴∠AGE=∠AGF=90°.
∵四边形ABCO是正方形,
∴AC⊥OB.
∵OA=AB,
∴∠FAG=EAG.
在△AFG和△AEG中,
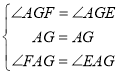 ,
,
∴△AFG≌△AEG(ASA),
∴S四边形OHGF=S△AOH-S△AFG=S△AOH-S△AEG.
设点A的坐标为(m,m),点E的坐标为(n,![]() ).
).
∵OA=AB,EF∥OB,
∴AG=GE,
∴m-![]() =n-m,即2m-n=
=n-m,即2m-n=![]() ,
,
∴S四边形OHGF=![]() m2-
m2-![]() (n-m)(m-
(n-m)(m-![]() )=
)=![]() m2-
m2-![]() mn+
mn+![]() +
+![]() m2-
m2-![]() =
=![]() m(2m-n)+
m(2m-n)+![]() -
-![]() =
=![]() +
+![]() -
-![]() =
=![]() .
.