Question

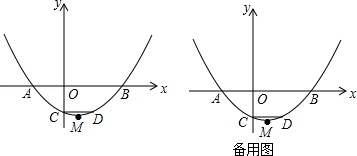
【题目】如图1，在平面直角坐标系xOy中，点A（ ，0），B（3 ，0），以AB为直径的⊙G交y轴于C，D两点.

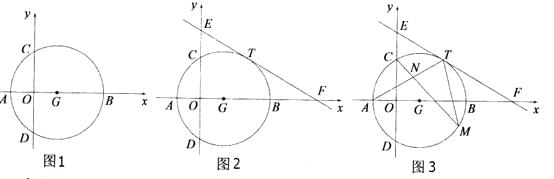
（1）填空：请直接写出⊙G的半径r，圆心G的坐标：r=；G（ ， ）.
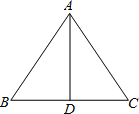
（2）如图2，直线y= 与x、y轴分别交于F、E两点，且经过圆上一点T（ ，m），求证：直线EF是⊙G的切线；
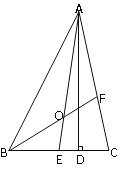
（3）在（2）的条件下，如图3，点M是⊙G优弧 上的一个动点（不包括A、T两点），连接AT、CM、TM，CM交AT于点N，试问，是否存在一个常数k，始终满足CN·CM=k？如果存在，请求出k的值，如果不存在，请说明理由.

Answer 1

【答案】
（1）；；0
（2）

解：如图，连接GT，过点T作TH⊥x轴于点H，直线y= 与x、y轴交于E、F两点，则易知：E（0,5），F（5 ，0），

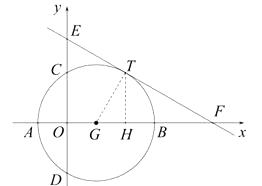
∵直线EF：y= 过点T（2 ，m），则

m= +5=3，∴T（2 ，3），

故TH=3，GH= ，HF=3 ，

在Rt△GHT中，有GT=r=2 ，

∴GH= GT，∴∠GTH=30°，

在在Rt△THF中，有tan∠FTH= = ，∴∠FTH=60°，

故∠GTF=∠GTH+∠FTH=30°+60°=90°，∴GT⊥EF，

∴直线EF是⊙G的切线.

（3）

解：存在.如图，连接 CG、CT、GT，在Rt△COG中，

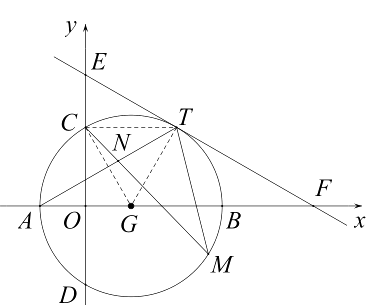
在Rt△COG中，OG= ，CG=r=2 ，

∴OC=3，∠CGO=60°，

由于C（0,3），T（2 ，3），故CT//x轴，

∴CT=2 ,

即CT=CG=GT=2 ，

∴△CGT是等边三角形，

∴∠CGT=∠TCG=∠CGA=60°，

∴∠CTA= ∠CGA=30°.

∴∠CTA=∠CMT，

在△CNT和△CTM中，∠TCA=∠MCT，∠CTN=∠CMT，

∴△CNT~△CTM，

∴ ，

∴CN·CM=CT2=（2 ）2=12，

故存在一个常数12，始终范围CN·CM=12，即：k=12.

【解析】解：（1）∵A（ ，0），B（3 ，0），
∴AB=3 -（ ）=4 ；
则r= AB= ，OG= - = ，则G（ ，0）.
【考点精析】本题主要考查了圆的定义和圆心角、弧、弦的关系的相关知识点，需要掌握平面上到定点的距离等于定长的所有点组成的图形叫做圆．定点称为圆心，定长称为半径；在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半才能正确解答此题．