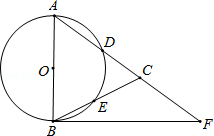
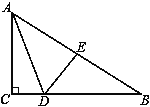
[题目]如图.在△ABC中.∠C=90°.E是AB的中点.且DE⊥AB于点E.∠CAD:∠EAD=1:2.则∠B与∠BAC的度数为( )A. 30°.60° B. 32°.58° C. 36°.54° D. 20°.70° 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在△ABC中，∠C=90°，E是AB的中点，且DE⊥AB于点E，∠CAD：∠EAD=1：2，则∠B与∠BAC的度数为（）

A. 30°，60° B. 32°，58° C. 36°，54° D. 20°，70°

【答案】C

【解析】

先设∠CAD=x，则∠EAD=2x，由于E是AB的中点，且DE⊥AB于点E，可知ED是AB的中垂线，再由其性质可得AD=AB，进而可知∠DAB=∠DBA，从而易得x+2x+2x=90°，解即可求x，进而可求∠B、∠CAB．

设∠CAD=x，则∠EAD=2x，

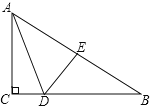
∵E是AB的中点，且DE⊥AB于点E，

∴ED是AB的中垂线，

∴AD=AB，

∴∠DAB=∠DBA，

∴x+2x+2x=90°，

解得x=18°，

∴∠B=2x=36°，∠CAB=90°36°=54°.

故选:C.

练习册系列答案

相关题目

【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF= ∠CAB．
（1）求证：直线BF是⊙O的切线；
（2）若AB=5，sin∠CBF= ，求BC和BF的长．

【题目】如图，在平面直角坐标系中，过点A（0，6）的直线AB与直线OC相交于点C（2，4）动点P沿路线O→C→B运动．（1）求直线AB的解析式；（2）当△OPB的面积是△OBC的面积的时，求出这时点P的坐标；（3）是否存在点P，使△OBP是直角三角形？若存在，直接写出点P的坐标，若不存在，请说明理由．

【题目】为增强市民的节能意识，我市试行阶梯电价.从2013年开始，按照每户每年的分三个档次计费，具体规定见下图.小明统计了自己2013年前5个月的实际用电量为1300度，请帮助小明分析下面问题.

（1）若小明家计划2013年全年的用电量不超过2520度，则6至12月份小明家平均每月用电量最多为多少度？（保留整数）

（2）若小明家2013年6月至12月份平均每月用电量等于前5个月的平均每月用电量，则小明家2013年应交总电费多少元？

【题目】如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．

求证：（1）MO=MB；（2）MN=CN﹣BM．

【题目】如图1，在平面直角坐标系xOy中，点A（，0），B（3 ，0），以AB为直径的⊙G交y轴于C，D两点.

（1）填空：请直接写出⊙G的半径r，圆心G的坐标：r=；G（，）.
（2）如图2，直线y= 与x、y轴分别交于F、E两点，且经过圆上一点T（，m），求证：直线EF是⊙G的切线；
（3）在（2）的条件下，如图3，点M是⊙G优弧上的一个动点（不包括A、T两点），连接AT、CM、TM，CM交AT于点N，试问，是否存在一个常数k，始终满足CN·CM=k？如果存在，请求出k的值，如果不存在，请说明理由.

【题目】《如果想毁掉一个孩子，就给他一部手机!》这是2017年微信圈一篇热传的文章．国际上，法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机．为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的统计图，已知“查资料”的人数是 40人．请你根据以上信息解答下列问题：

(1)在扇形统计图中，“玩游戏”对应的百分比为______，圆心角度数是______度；

(2)补全条形统计图；

(3)该校共有学生2100人，估计每周使用手机时间在2 小时以上(不含2小时)的人数．

【题目】为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了天的调查，将所得数据绘制成如下统计图（图2不完整）：

请根据所给信息，解答下列问题：
（1）第天，这一路口的行人交通违章次数是多少次？这天中，行人交通违章次的有多少天？
（2）请把图2中的频数直方图补充完整；
（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？

【题目】如图，直线：与直线：相交于点P（1，b）

（1）求b，m的值
（2）垂直于x轴的直线与直线，分别相交于C，D，若线段CD长为2，求a的值

试题分类