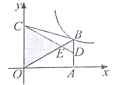
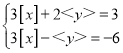��Ŀ����
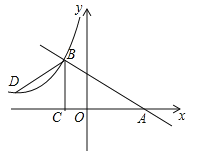
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��AOC��65������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE��90����
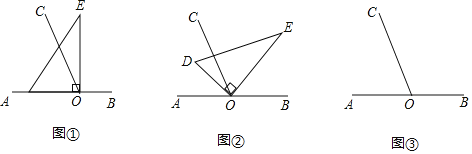
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OA�ϣ����COE�� ������
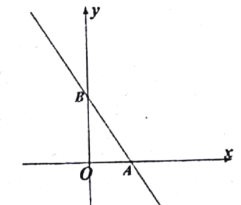
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O˳ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�AOE�����COD���� ������
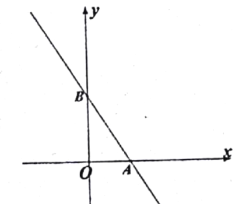
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�O˳ʱ�뷽��ת����ij��λ�ã�0������AOD��180���������COD��![]() ��AOE�����COD�Ķ�����
��AOE�����COD�Ķ�����
���𰸡���1��25����2��25����3��51��
��������
��1�����ݻ��������𰸣�
��2���ɽ�ƽ���ߵ���COE����AOC��65����������COD����DOE����COE����𰸣�
��3����δ֪��������������⼴�ɣ�
�⣺��1����COE����DOE����AOC��90����65����25����
�ʴ�Ϊ��25��
��2����OCǡ��ƽ����AOE��
���COE����AOC��65����
���COD����DOE����COE��90����65����25����
�ʴ�Ϊ��25��
��3������COD��x��������ã�
��COD��![]() ��AOE������x��
��AOE������x��![]() ��65��+x+90������
��65��+x+90������
��ã�x��51����������COD��51��

��ϰ��ϵ�д�
�����Ŀ