Question

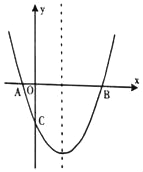
【题目】已知:直线经过点A(-5.-6)且与直线: y=-x+6平行,直线与x轴、y轴分别交于点B，C

(1)求直线的表达式及其与x轴的交点D的坐标:

(2)判断四边形ABCD是什么四边形?并证明你的结论:

(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标. 请直接写出答案.

Answer 1

【答案】（1）直线l1的表达式：y＝x，D的坐标为：（9，0）；（2）四边形ABCD是矩形，证明见解析；（3）E1（2，4），E2（10，4）.

【解析】

（1）根据直线l1与直线平行，可设直线l1的表达式为：y＝x＋b，代入A（5，6）求出直线l1的表达式和点D的坐标即可；

（2）首先根据题意求出点B、C的坐标，利用两点间距离公式求出AD，BC，AB，BD，根据AD＝BC，AD∥BC先判定四边形ABCD是平行四边形，再利用勾股定理逆定理证明∠DAB＝90°即可；

（3）求出直线AB的解析式，根据正方形的性质可得EB＝BC＝，根据两点间距离公式列方程求解，即可得到相应的点E的坐标．

解：（1）设直线l1的表达式为：y＝x＋b，

∵直线l1经过点A（5，6），

∴6＝×（5）＋b，解得b＝，

即直线l1的表达式是y＝x，

当y＝0时，0＝x，解得x＝9，

即点D的坐标为（9，0）；

（2）四边形ABCD是矩形，

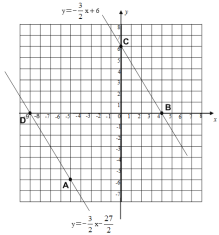
证明：∵直线l2：y＝x＋6，直线l2与x轴、y轴分别交于点B、C两点，

∴点B（4，0），点C（0，6），

∵点A（5，6），点D（9，0），

∴AD＝，BC＝，

∴AD＝BC，

∵AD∥BC，

∴四边形ABCD是平行四边形，

∵AB＝，BD＝4（9）＝13，AD＝，

∴AB2＋AD2＝()2＋()2＝132＝BD2，

∴∠DAB＝90°，

∴平行四边形ABCD是矩形；

（3）E1（2，4），E2（10，4），

∵点A（5，6），点B（4，0），

设直线A、B的解析式为y＝kx＋b，

则，解得：，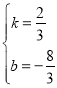

即直线AB的解析式为y＝x，

∵点E在直线AB上，

∴设点E的坐标为（a，a），

∵四边形CBEF是正方形，点B（4，0），点C（0，6），

∴EB＝BC＝，

∴，

解得：a＝2或a＝10，

当a＝2时，a＝-4，

当a＝10时，a＝4，

∴点E1（2，4），E2（10，4）．