题目内容
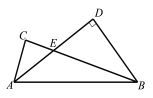
【题目】如图,在![]() 中, AD平分∠CAB交BC于点E. 若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为( )
中, AD平分∠CAB交BC于点E. 若∠BDA=90°,E是AD中点,DE=2,AB=5,则AC的长为( )
A.1B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过点C作CF⊥AD于F,易求AE=2,AD=4,BD=![]() =3由角平分线性质得出∠CAF=∠DAB,由tan∠DAB=
=3由角平分线性质得出∠CAF=∠DAB,由tan∠DAB=![]() ,推出
,推出![]() ,则AF=
,则AF=![]() ,由tan∠BED=
,由tan∠BED=![]() ,∠CEF=∠BED,得出
,∠CEF=∠BED,得出![]() 则EF=
则EF=![]() ,由AF+EF=AE=2,求出CF=1,AF=
,由AF+EF=AE=2,求出CF=1,AF=![]() ,则AC=
,则AC=![]() .
.
解:过点C作CF⊥AD于F,如图所示:
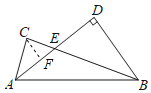
∵E是AD中点,DE=2,
∴AE=2,AD=4,BD=![]() =3
=3
∵AD平分∠CAB,
∴∠CAF=∠DAB,
∵tan∠DAB=![]()
∴![]()
∴AF=![]()
∵tan∠BED=![]() ,∠CEF=∠BED,
,∠CEF=∠BED,
∴![]() 则EF=
则EF=![]() ,
,
∵AF+EF=AE=2,
![]()
∴CF=1,AF=![]() ,
,
∴AC=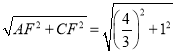 =
=![]() .
.
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】请借鉴以前研究函数的经验,探索函数y=![]() +2的图象和性质.
+2的图象和性质.
(1)自变量x的取值范围为 ;
(2)填写下表,画出函数的图象;
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
y | … | 1 | 0.8 | 0.5 | ﹣1 | ﹣4 | 8 |
(3)观察图象,写出该函数两条不同类型的性质;
(4)若x>3,则y的取值范围为 ;若y<﹣1,则x的取值范围为 .