题目内容
【题目】请借鉴以前研究函数的经验,探索函数y=![]() +2的图象和性质.
+2的图象和性质.
(1)自变量x的取值范围为 ;
(2)填写下表,画出函数的图象;
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
y | … | 1 | 0.8 | 0.5 | ﹣1 | ﹣4 | 8 |
(3)观察图象,写出该函数两条不同类型的性质;
(4)若x>3,则y的取值范围为 ;若y<﹣1,则x的取值范围为 .

【答案】(1)x≠1;(2)见解析;(3) 当x>1时,y随x的增大而减小;图象关于点(1,2)中心对称;(4)﹣1<x<1.
【解析】
(1)分母不等于0即可得;
(2)将x=﹣2,3,4,5,6,7分别代入解析式即可得y的值,再画出函数的图象;
(3)结合图象可从函数的增减性、与y轴交点情况及对称性解答均可;
(4)结合图象可得取值范围.
解:(1)依题意有x1≠0,
解得x≠1.
故自变量x的取值范围为x≠1.
(2)填表如下:
x | … | 5 | 4 | 3 | 2 | 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | … |
y | … | 1 | 0.8 | 0.5 | 0 | 1 | 4 | 8 | 5 | 4 | 3.5 | 3.2 | 3 |
如图所示:
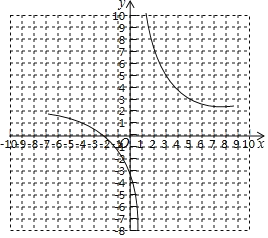
(3)当x>1时,y随x的增大而减小;
图象关于点(1,2)中心对称,
(4)若x>3,则y的取值范围为2<y<5;若y<1,则x的取值范围为1<x<1.
故答案为:x≠1;2<y<5,1<x<1.

练习册系列答案
相关题目