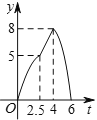ЬтФПФкШн
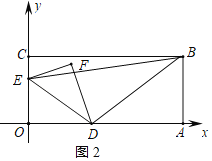
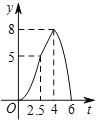
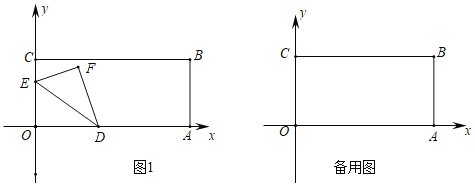
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌОиаЮOABCЕФЖЅЕуAдкxжсЩЯЃЌЕуCдкyжсЩЯЃЌЕуBЕФзјБъЮЊЃЈ8ЃЌ4ЃЉЃЌЖЏЕуDДгЕуOЯђЕуAвдУПУыСНИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌЖЏЕуEДгЕуCЯђЕуOвдУПУывЛИіЕЅЮЛЕФЫйЖШдЫЖЏЃЌЩшDЁЂEСНЕуЭЌЪБГіЗЂЃЌдЫЖЏЪБМфЮЊtУыЃЌНЋЁїODEбиDEЗелЕУЕНЁїFDEЃЎ
ЃЈ1ЃЉШєЫФБпаЮODFEЮЊе§ЗНаЮЃЌЧѓtЕФжЕЃЛ
ЃЈ2ЃЉШєtЃН2ЃЌЪджЄУїAЁЂFЁЂCШ§ЕудкЭЌвЛжБЯпЩЯЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§tЃЌЪЙЁїBDEЕФУцЛ§зюаЁЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉtЃН![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉДцдкЪЕЪ§tЃЌЪЙЁїBDEЕФУцЛ§зюаЁЃЌtЃН2УыЃЎРэгЩМћНтЮі.
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉДцдкЪЕЪ§tЃЌЪЙЁїBDEЕФУцЛ§зюаЁЃЌtЃН2УыЃЎРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩе§ЗНаЮЕФаджЪЕУГіOEЁЮDFЃЌOE=DFгЩелЕўЕФаджЪЕУГіOD=DFЃЌгЩOD=2tЃЌOE=4-tЃЌЕУГіЗНГЬ2t=4-tЃЌНтЗНГЬМДПЩЃЛ
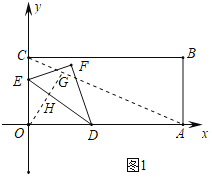
ЃЈ2ЃЉСЌНгACЃЌзїOGЁЭACгкGЃЌгЩt=2ЃЌЕУГіOE=CE=2ЃЌOD=DA=4ЃЌгЩШ§НЧаЮжаЮЛЯпЖЈРэЕУГіDEЁЮACЃЌЧвDE=![]() ACЃЌгЩЦНааЯпЕУГі
ACЃЌгЩЦНааЯпЕУГі![]() ЃЌЕУГіDEДЙжБЦНЗжOFЃЌЕУГіGгыFЕужиКЯЃЌМДПЩЕУГіНсТлЃЛ
ЃЌЕУГіDEДЙжБЦНЗжOFЃЌЕУГіGгыFЕужиКЯЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉгЩЬтвтЕУГіSЁїBDE=SОиаЮOABC-SЁїBCE-SЁїABD-SЁїODE=t2-4t+16ЃЌгЩЖўДЮКЏЪ§ЕФаджЪМДПЩЕУГіНсЙћЃЎ
ЃЈ1ЃЉНтЃКЁпОиаЮOABCжаЃЌBЃЈ8ЃЌ4ЃЉЃЌ
ЁрOAЃН8ЃЌOCЃН4ЃЌ
ЁпЫФБпаЮODEFЮЊе§ЗНаЮЃЌ
ЁрOEЁЮDFЃЌOEЃНDFЃЌ
ЁпЁїODEбиDEЗелЕУЕНЁїFDEЃЌ
ЁрODЃНDFЃЌ
ЁпODЃН2tЃЌOEЃН4ЉtЃЌ
Ёр2tЃН4ЉtЃЌtЃН![]() ЃЛ
ЃЛ
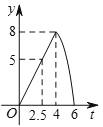
ЃЈ2ЃЉжЄУїЃКСЌНгACЃЌзїOGЁЭACгкGЃЌШчЭМ1ЫљЪОЃК
ЁпtЃН2ЃЌ
ЁрOEЃНBEЃН2ЃЌODЃНDEЃН4ЃЌ
ЁрDEЪЧЁїOACЕФжаЮЛЯпЃЌ
ЁрDEЁЮACЃЌЧвDEЃН![]() ACЃЌ
ACЃЌ
Ёр![]()
ЁрDEДЙжБЦНЗжOFЃЌ
гЩелЕўЕФаджЪЕУЃКDEДЙжБЦНЗжOFЃЌ
ЁрGгыFЕужиКЯЃЌ
МДAЁЂCЁЂFШ§ЕудкЭЌвЛЬѕжБЯпЃЛ
ЃЈ3ЃЉНтЃКДцдкЃЌРэгЩШчЯТЃКШчЭМ2ЫљЪОЃК
ЁпSЁїBDEЃНSЁїABCЉSЁїBCEЉSЁїABDЉSЁїODE
ЃН![]()
ЃН32Љ4tЉ16+4tЉ4t+t2
ЃНt2Љ4t+16
ЃНЃЈtЉ2ЃЉ2+12ЃЌ
ЁрtЃН2ЪБЃЌSЁїBDEгазюаЁжЕЮЊ12ЃЛ
МДДцдкЪЕЪ§tЃЌЪЙЁїBDEЕФУцЛ§зюаЁЃЌtЃН2УыЃЎ