Question

【题目】如图，与相切于点，为的弦，，与相交于点；

（1）求证：；

（2）若，，求线段的长．

Answer 1

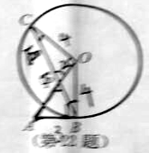
【答案】(1)详见解析；（2）BP=.

【解析】

试题分析：(1)根据已知条件易得∠ABP+∠OBC=90°，∠C+∠CPO=90°，因为∠APB=∠CPO， 即可得∠C+∠APB=90°，再由∠C=∠OBC,即可得∠ABP=∠APB,所以AP=AB；（2）过点A作ADBP，垂足为D，所以∠ADP=90°，PD=BP，由勾股定理求得OA的长，再由勾股定理求得CP的长，由∠ADP=∠CPO，∠ADP=∠COP，证得△ADP∽△COP，根据相似三角形的性质求得PD的长，即可得BP的长.

试题解析：（1）因为与相切于点，所以,∠ABP+∠OBC=90°，

因为，所以∠C+∠CPO=90°，

因为∠APB=∠CPO，所以∠C+∠APB=90°，

因为OC=OB，所以∠C=∠OBC,

所以∠ABP=∠APB,

因此AP=AB.

(2) 过点A作ADBP，垂足为D，所以∠ADP=90°，PD=BP

因为∠ABO=90°，，，所以,故OA=5

因为AP=AB=3，所以OP=OA-AP=2

因为∠COP=90°，所以,

因为∠ADP=∠CPO，∠ADP=∠COP，所以△ADP∽△COP.

所以,即PD= ，所以BP=.