题目内容
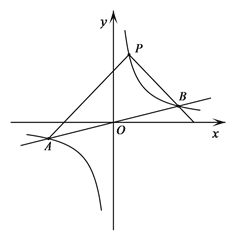
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
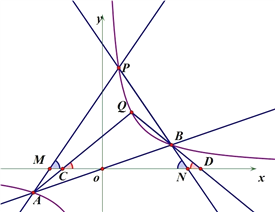
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
【答案】(1)k=4,S△PAB=15;(2)证明见解析;(3)∠PAQ=∠PBQ.
【解析】试题分析:(1)根据题意求出B点的坐标,然后利用待定系数法可求k的值;
(2)过点P作PH⊥x轴于H,然后根据反比例函数的解析式设出P点的坐标,然后可得方程组,求出PA、PB的解析式,然后得含m、n的点M、N的坐标,然后根据线段垂直平分线的性质可求证;
(3)同(2)方法,利用等边对等角和三角形的外角可证.
试题解析:(1)根据B点的横坐标求出B点的 (4,1),

(3) 同理可证,QC=QD,
利用等边对等角和三角形的外角可证。如图。

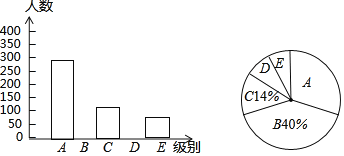
【题目】某报社为了了解市民“获取新闻的最主要途径”,开展了一次抽样调查,根据调查结果绘制了如图三种不完整的统计图表.
组别 | 获取新闻的最主要途径 | 人数 |
A | 电脑上网 | 280 |
B | 手机上网 | m |
C | 电视 | 140 |
D | 报纸 | n |
E | 其它 | 80 |
请根据图表信息解答下列问题:
(1)统计表中的m= ,n= ,并请补全条形统计图;
(2)扇形统计图中“D”所对应的圆心角的度数是 ;
(3)若该市约有120万人,请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数.
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
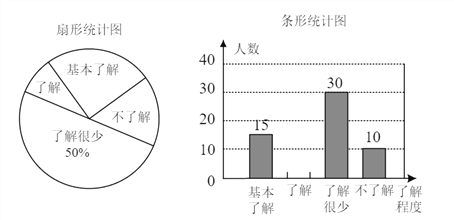
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】(1)60;90°;(2)补图见解析;(3)300;(4)![]()
【解析】分析:(1)根据了解很少的人数除以了解很少的人数所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角的度数;(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;(3)用总人数乘以“了解”和“基本了解”程度的人数所占的比例,即可求出达到“了解”和“基本了解”程度的总人数;(4)根据题意列出表格,再根据概率公式即可得出答案.
详解:(1)60;90°.
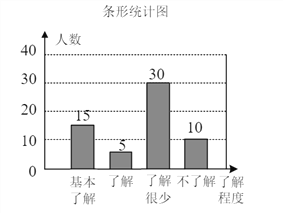
(2)补全的条形统计图如图所示.
(3)对食品安全知识达到“了解”和“基本了解”的学生所占比例为![]() ,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为
,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为![]() .
.
(4)列表法如表所示,
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情况一共12种,其中选中1个男生和1个女生的情况有8种,所以恰好选中1个男生和1个女生的概率是![]() .
.
点睛:本题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,根据题意求出总人数是解题的关键;注意运用概率公式:概率=所求情况数与总情况数之比.
【题型】解答题
【结束】
24
【题目】为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2015年图书借阅总量是7500本,2017年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2015年至2017年的年平均增长率.
(2)已知2017年该社区居民借阅图书人数有1350人,预计2018年达到1440人,如果2017年至2018年图书借阅总量的增长率不低于2015年至2017年的年平均增长率,设2018年的人均借阅量比2017年增长a%,求a的值至少是多少?
【题目】某校举行猜谜语大赛,甲、乙两队各有5名选手参赛。他们的成绩(满分100分,两个1号队员的成绩均未统计)如图所示

成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 优秀率 | |
甲队 | 85 | 85 | 70 | 80% | |
乙队 | 85 | 160 |
根据以上材料
(1)计算出甲、乙两队1号选手的成绩;
(2)补充完成成绩统计图和成绩统计分析表.