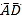题目内容
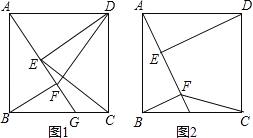
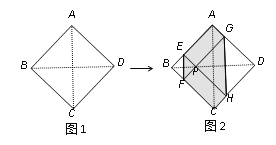
【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
A. ①③ B. ①②④ C. ①③④ D. ①②③④
【答案】C
【解析】(1)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF和△DGH是等腰直角三角形,∴当AE=1时,重合点P是BD的中点,∴点P是正方形ABCD的中心;故①结论正确;
(2)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF∽△BAC,∵x=![]() ,∴BE=2﹣
,∴BE=2﹣![]() =
=![]() ,∴
,∴![]() ,即
,即![]() ,∴EF=
,∴EF=![]() AC,同理,GH=
AC,同理,GH=![]() AC,∴EF+GH=AC,故②结论错误;
AC,∴EF+GH=AC,故②结论错误;
(3)六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积.∵AE=x,∴六边形AEFCHG面积=22﹣![]() BEBF﹣
BEBF﹣![]() GDHD=4﹣
GDHD=4﹣![]() ×(2﹣x)(2﹣x)﹣
×(2﹣x)(2﹣x)﹣![]() xx=﹣x2+2x+2=﹣(x﹣1)2+3,∴六边形AEFCHG面积的最大值是3,故③结论正确;
xx=﹣x2+2x+2=﹣(x﹣1)2+3,∴六边形AEFCHG面积的最大值是3,故③结论正确;
(4)当0<x<2时,∵EF+GH=AC,六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=(AE+CH)+(FC+AG)+(EF+GH)=2+2+2![]() =4+2
=4+2![]() 故六边形AEFCHG周长的值不变,故④结论正确.
故六边形AEFCHG周长的值不变,故④结论正确.
故选C.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目