题目内容
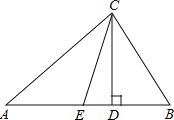
【题目】△ABC中，BC＝10，AC﹣AB＝6．过C作∠BAC的角平分线的垂线，则S△BDC的最大值为（ ）
A.10B.15C.20D.25
【答案】B
【解析】
如图，延长AB，CD交点于E，可证AC＝AE，DE＝CD，则S△BDC＝
S△BCE，当BE⊥BC时，S△BEC的面积最大，求出此时△BEC的面积即可解决问题．
解：如图，延长AB，CD交点于E，
∵AD平分∠BAC，∴∠CAD＝∠EAD；
∵∠ADC＝∠ADE＝90°，AD＝AD，∠CAD＝∠EAD，
∴△ADC≌△ADE（ASA），
∴AC＝AE，DC＝DE；
∵AC﹣AB＝6，
∴AE﹣AB＝6，即BE＝6.
∵DE＝DC，
∴S△BDC＝S△BEC，
∴当BE⊥BC时，S△BEC面积最大，此时S△BEC=
；
所以S△BDC最大＝×30＝15．
故选：B．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
