Question

【题目】定义：有一条对角线平分一组对角的四边形叫做筝形．

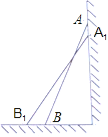
探究：（1）如图1，四边形ABCD中，AB＝BC，AD＝DC，求证：四边形ABCD是筝形；

（2）下列关于筝形的性质表述正确的是 ；（把你认为正确的序号填在横线上）

①筝形的对角线互相垂直平分； ②筝形中至少有一对对角相等；

③筝形是轴对称图形； ④筝形的面积等于两条对角线长的积的一半．

应用：

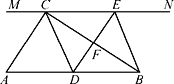
（3）如图2，在筝形ABCD中，AB≠AD，若∠ABC＝60°，∠ADC＝30°，AD＝4，请求出对角线BD的长．

Answer 1

【答案】（1）详见解析；（2）②③④；（3）4

【解析】

（1）利用SSS证明△ABD≌△CBD即可；（2）①筝形的对角线只互相垂直，没有平分，故错误；②筝形中有一条对角线平分一组对角，所以至少有一对对角相等，正确；③筝形是轴对称图形；④筝形的面积被一条对角线平分，且两条对角线互相垂直，所以筝形的面积等于两条对角线长的积的一半，正确；（3）过D作DE⊥BA交BA延长线于点E，求得

∠ABD＝30°，∠ADB＝15°，∠DAE＝45°，即△ABE为等腰直角三角形，则可求出DE，然后再求出BD即可.

（1）∵AB＝BC，AD＝DC，BD＝BD，∴△ABD≌△CBD（SSS），∴∠ABD＝∠CBD，∠ADB＝∠CDB，∴四边形ABCD是筝形．

（2）②③④

（3）过D作DE⊥BA交BA延长线于点E.

在筝形ABCD中，AB≠AD，∴BD平分∠ABC，平分∠ADC，∴∠ABD＝∠ABC＝30°，∠ADB＝∠ADC＝15°，∴∠DAE＝45°. 在等腰直角△ABE∵AD＝4，∴DE＝2，

故在Rt△BDE中BD＝4.