题目内容
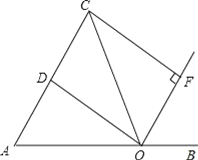
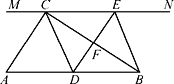
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】分析:(1)由BC⊥AC,DE⊥BC,得到DE∥AC,从而判断出四边形ADEC是平行四边形.即可,
(2)先判断出△BFD≌△CFE,再判断出BC和DE垂直且互相平分,得到四边形BECD是菱形.
(3)先判断出∠CDB=90°,从而得到有一个角是直角的菱形是正方形.
解析:(1)证明:∵直线m∥AB,
∴EC∥AD.
又∵∠ACB=90°,
∴BC⊥AC.
又∵DE⊥BC,
∴DE∥AC.
∵EC∥AD,DE∥AC,
∴四边形ADEC是平行四边形.
∴CE=AD.
(2)当点D是AB中点时,四边形BECD是菱形.
证明:∵ D是AB中点,
∴DB=DA
又∵直线m∥AB,CE=AD
∴DB= CE,DB ∥ CE
∴四边形BDCE是平行四边形
又∵DE⊥BC
∴四边形BECD是菱形
(3)当∠A的大小是45°时,四边形BECD是正方形.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目