题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 中点.
中点.
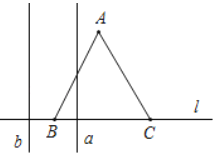
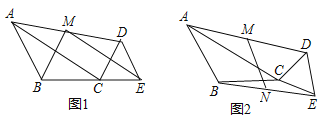
(1)如图1,当![]() ,
,![]() ,
,![]() 三点共线时,请画出
三点共线时,请画出![]() 关于点
关于点![]() 的中心对称图形,判断
的中心对称图形,判断![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)如图2,当A,![]() ,
,![]() 三点共线时,问(1)中结论是否成立,若成立,给出证明,若不成立,请说明理由;
三点共线时,问(1)中结论是否成立,若成立,给出证明,若不成立,请说明理由;
(3)如图2,取![]() 中点
中点![]() ,连
,连![]() ,将
,将![]() 绕点
绕点![]() 旋转,直接写出旋转过程中线段
旋转,直接写出旋转过程中线段![]() 的取值范围是 .
的取值范围是 .
【答案】(1)图见解析,BM⊥ME;(2)结论成立,理由见解析;(3)![]() -1≤MN≤
-1≤MN≤![]() +1
+1
【解析】
(1)先作出图形,进而证明△AMF≌△DME,即可得出结论;
(2)同(1)的方法得出△AMF≌△DMF,利用四边形的内角和定理及平角的定义得出∠BCE=∠BAF即可得出△AFB≌△CEB,从而求证;
(3)同(2)的方法得出∠BME=90°,进而得出BE=2MN,最后用三角形的三边关系即可得出结论.
解:(1)证明:如图1,
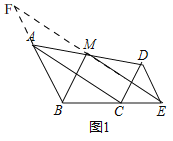
延长BA,EM交于点F,即:△FAM即为所求,
∵△CDE是等边三角形,
∴CD=CE=DE,∠CED=60°,
∵∠ABC=120°,
∴∠ABC+∠CED=180°,
∵B,C,E三点共线,
∴AB∥DE,
∴∠FAM=∠MDE,∠MED=∠F,
∵点M是AD中点,
∴AM=DM,
∴△AMF≌△DME,
∴AF=DE=CE,FM=ME,
∵AB=BC,
∴BF=BE,
∴BM⊥ME;
(2)证明:如图2,延长EM到点F,使MF=ME,连接BF,AF,BE
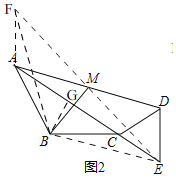
∵AM=DM,∠FMA=∠DME,
∴△AMF≌△DMF,
∴AF=DE=CE,∠FAD=∠ADE,
在四边形BADE中,∵∠BAD+∠ADE+∠DEB+∠EBA=360°,
∵∠ABC=120°,∠CED=60°,
∴∠CBE+∠CEB+∠BAD+∠ADE=180°,
∵∠CBE+∠CEB+∠BCE=180°,
∴∠BCE=∠BAD+∠ADE,
∴∠BCE=∠BAF,
∵AB=AC,
∴△AFB≌△CEB,
∴BF=BE
∴BM⊥ME;
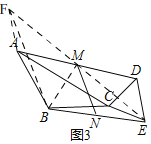
(3)如图3,延长EM到点F,使MF=ME,连接BF,AF,BM,
∵AM=DM,∠FMA=∠DME,
∴△AMF≌△DME,
∴AF=DE=CE,∠FAD=∠ADE,
在四边形BADE中,∵∠BAD+∠ADE+∠DEB+∠EBA=360°,
∵∠ABC=120°,∠CED=60°,
∴∠CBE+∠CEB+∠BAD+∠ADE=180°,
∵∠CBE+∠CEB+∠BCE=180°,
∴∠BCE=∠BAD+∠ADE,
∴∠BCE=∠BAF,
∵AB=CB,
∴△AFB≌△CEB,
∴BF=BE,∠ABF=∠CBE,
∴∠FBE=∠ABC=120°,∠BEF=30°,
∴∠BME=90°,
∵点N是BE的中点,
∴MN=![]() BE,
BE,
即:BE=2MN,
在△BCE中,BC=2![]() ,CE=CD=2,
,CE=CD=2,
∴2![]() -2<BE<2
-2<BE<2![]() +2
+2
∴2![]() -2<2MN<2
-2<2MN<2![]() +2,
+2,
即:![]() -1≤MN≤
-1≤MN≤![]() +1,
+1,
故答案为:![]() -1≤MN≤
-1≤MN≤![]() +1
+1

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案