题目内容
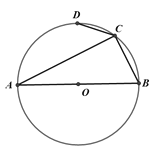
【题目】在⊙O中，AB为直径，∠ACD=45°，已知AC=7，BC=5，则CD =_______
【答案】
或
【解析】
分情况讨论，过点A作AM⊥CD，过点B作BN⊥CD，连接AD,BD，通过证明△MAC,△NBC，△ABD均为等腰直角三角形和△MAD≌△NDB求解.
解：如图：过点A作AM⊥CD，过点B作BN⊥CD，连接AD,BD
∵
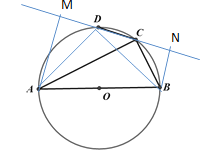
且AB是圆的直径
∴△MAC,△NBC，△ABD均为等腰直角三角形
∴AD=BD
∵AM⊥CD， BN⊥CD
∴
又∵
∴
∴△MAD≌△NDB
∴DN=AM
又∵△MAC,△NBC均为等腰直角三角形
∴
, 
∴
;
如图：过点A作AM⊥CD，过点B作BN⊥CD，连接AD,BD
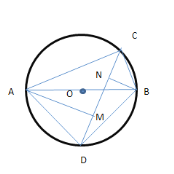
同理可证，此时
故答案为： 或
【题目】小东根据学习函数的经验，对函数
的图像与性质进行了探究，下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数的自变量x的取值范围是__________________
（2）如表示y与x的几组对应值：
x | … |
|
|
|
|
|
|
|
|
|
|
| … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
表中m的值为____________
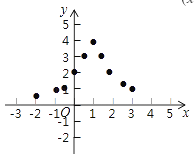
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出函数的大致图像；
（4）结合函数图像，请写出函数的2条性质：
①__________________________________________________________________________
②__________________________________________________________________________
（5）解决问题：如果函数与直线
的交点有2个，那么a的取值范围是_______________________
（6）
在函数图像上，若
，则m的取值范围______________
