Question

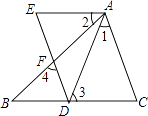
【题目】如图，△ABC中∠A=30°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC于点D，又将△BCD沿着BD翻折，C点恰好落在BE上，此时∠CDB=82°，则原三角形的∠B为（ ）
A.75°
B.76°
C.77°
D.78°

Answer 1

【答案】D
【解析】解：在△ABC中，∠A=30°，则∠B+∠C=150°…①； 根据折叠的性质知：∠B=3∠CBD，∠BCD=∠C；
在△CBD中，则有：∠CBD+∠BCD=180°﹣82°，即： ∠B+∠C=98°…②；
①﹣②，得： ∠B=52°，
解得∠B=78°．
故选D．
【考点精析】关于本题考查的翻折变换（折叠问题），需要了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能得出正确答案．