题目内容
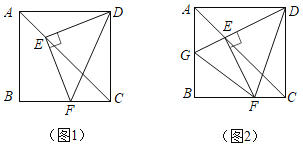
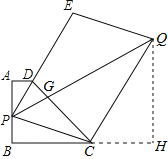
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.

【答案】7
【解析】分析:设PQ与DC相交于点G,PE∥CQ,PD=DE,可得![]() =
=![]() ,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案.
,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案.
详解:设PQ与DC相交于点G,
∵PE∥CQ,PD=DE,
∴![]() =
=![]() ,
,
∴G是DC上一定点,
作QH⊥BC,交BC的延长线于H,
同理可证∠ADP=∠QCH,
∴Rt△ADP∽Rt△HCQ,
即∴![]() =
=![]() ,
,
∴CH=3,
∴BH=BC+CH=4+3=7,
∴当PQ⊥AB时,PQ的长最小,即为7.
故答案为:7.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目