题目内容
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当![]() ,
,![]() 时,∵
时,∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号.请利用上述结论解决以下问题:
时取等号.请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为_______;当
的最小值为_______;当![]() 时,
时,![]() 的最大值为__________.
的最大值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)如图,四边形ABCD的对角线AC ,BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.

【答案】(1)2,-2;(2)11;(3)25
【解析】
(1)当x>0时,按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算即可;x<0时,由于-x>0,-
(当且仅当a=b时取等号)来计算即可;x<0时,由于-x>0,-![]() >0,则也可以按照公式a+b≥2
>0,则也可以按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算;
(当且仅当a=b时取等号)来计算;
(2)将![]() 的分子分别除以分母,展开,将含x的项用题中所给公式求得最小值,再加上常数即可;
的分子分别除以分母,展开,将含x的项用题中所给公式求得最小值,再加上常数即可;
(3)设S△BOC=x,已知S△AOB=4,S△COD=9,则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD,用含x的式子表示出S△AOD,四边形ABCD的面积用含x的代数式表示出来,再按照题中所给公式求得最小值,加上常数即可.
解:(1)当x>0时,![]()
当x<0时,![]()
∵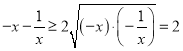
∴![]()
∴当![]() 时,
时,![]() 的最小值为2;当
的最小值为2;当![]() 时,
时,![]() 的最大值为-2;
的最大值为-2;
(2)由![]()
∵x>0,
∴![]()
当![]() 时,最小值为11;
时,最小值为11;
(3)设S△BOC=x,已知S△AOB=4,S△COD=9
则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD
∴x:9=4:S△AOD
∴:S△AOD=![]()
∴四边形ABCD面积=4+9+x+![]()
当且仅当x=6时取等号,即四边形ABCD面积的最小值为25.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目