题目内容
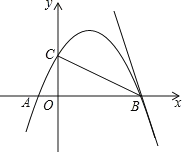
【题目】如图， 在平面直角坐标系中， 
的顶点
与原点重合，点
在
轴的正半轴上，
按以下步骤作图：①以点为圆心，适当长度为半径作
弧，分别交边
，
于点
，
；②分别以点，为圆心，大于
的长为半径作弧， 两弧在
内交于点
；③作射线
，交边
于点
．若
，
，则点的坐标为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由题意知，射线OP为∠AOC的平分线，做辅助线CJ⊥AO于J，DK⊥AO于K，BL⊥AO于L，由角平分线定理可得
，在直角三角形AKD中，用勾股定理可得
；根据所作垂线的性质可得CK∥DK，由平行线分线段成比例的性质，可求
，
；易证
，从而根据相似三角形对应边成比例的性质，易得
,在Rt△AOC中，有勾股定理可求出
，进而可得
；由以上分析即可得点B的坐标．
解：如图，分别过C、D、B点作CJ⊥AO于J，DK⊥AO于K，BL⊥AO于L，
∵在
中，则
；
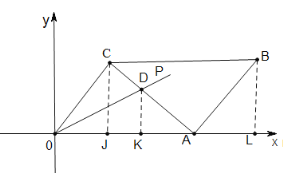
∵射线OP为∠AOC的平分线，
，DK⊥AO，
，
，
∴
∴
；
∵CJ⊥AO，DK⊥AO ，
∴CK∥DK，
∴
，
∴
，
，
∴，即B点的纵坐标为
；
∵
，
，
∴
，
又
，
∴，
∴
，
∴
,
∴
,
∴
,
∴
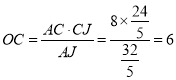,即B点的横坐标为
；
综上所述，点B 的坐标为
．
故选D．
练习册系列答案
相关题目
【题目】为了迎接疫情彻底结束后的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知：用
元购进甲种运动鞋的数量与用
元购进乙种运动鞋的数量相同．
求
的值；
要使购进的甲、乙两种运动鞋共
双的总利润(利润
售价
进价)不少于
元，且甲种运动鞋的数量不超过
双，问该专卖店共有几种进货方案；
在的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠
元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？
