题目内容
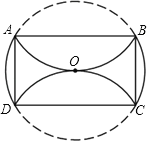
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
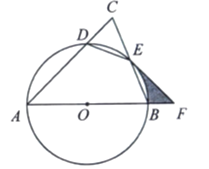
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 时,求图中阴影部分的面积.
时,求图中阴影部分的面积.
【答案】(1)详见解析;(2)115°;(3)4-π.
【解析】
(1)利用等腰三角形的性质,底边上的高也是底边上的中线;(2)先求出∠BAE,再利用圆内接四边形的对角互补即可得出结论;(3)先利用切线得出∠OEF=90°,从而得出等腰直角三角形,再用面积之差求出阴影部分面积.
(1)如图,连接AE,
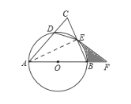
∵AB是O的直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE;
(2)由(1)知,∠BAE=![]() ∠BAC=25°,
∠BAC=25°,
∴∠ABE=90°∠BAE=65°,
∵四边形ABED是圆内接四边形,
∴∠ADE=180°∠ABE=115°;
(3)连接OE,
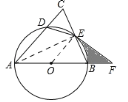
∵EF且O于E,
∴OE⊥EF,
∵AO=EF=OE=![]() ,
,
∴∠BOE=45°,
∴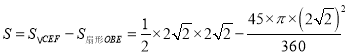 =
=![]() .
.

练习册系列答案
相关题目