Question

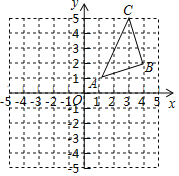
【题目】已知：如图，抛物线y＝ax2+bx﹣3与x轴交于A点，与y轴交于C点，且A（1，0）、B（3，0），点D是抛物线的顶点．

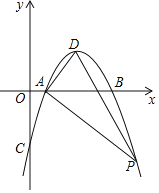
（1）求抛物线的解析式

（2）在y轴上是否存在M点，使得△MAC是以AC为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．

（3）点P为抛物线上的动点，且在对称轴右侧，若△ADP面积为3，求点P的坐标．

Answer 1

【答案】（1）y＝﹣x2+4x﹣3；（2）在y轴上存在点M，点M的坐标为(0,3)，(0,)或(0,)，（3）P（4，﹣3）．

【解析】

（1）将A（1，0），B（3，0）代入抛物线的解析式中即可求出抛物线的解析式；

（2）根据A、C的坐标求出AC的长度，再根据等腰三角形的腰分类讨论即可；

（3）过点P作y轴的平行线，与x轴交于点N，与AD的延长线交于点Q，过D作DH⊥PQ，先利用待定系数法求出直线AD的关系式，设P（x，﹣x2+4x﹣3），则Q（x，x﹣1），N（x，0），H（x，1），即可表示出PQ，AN和BN的长，再根据S△ADP＝S△APQ﹣S△PQD列方程并解方程即可.

（1）将A（1，0），B（3，0）代入抛物线y＝ax2+bx﹣3中，解得：，

∴抛物线的解析式为y＝﹣x2+4x﹣3；

（2）当x=0时，y=﹣3

故C点坐标为（0，﹣3）

∵A（1，0），

∴OA＝1，OC＝3

∴，

等腰△MAC中，点M在y轴上，AC是腰，分两种情况：

①当AC＝AM时，此时OA垂直平分MC

∴OM＝OC＝3

∴M（0，3），

②当AC＝CM时，有

设M（0，y）

则

∴

∴，

综上：在y轴上存在点M，点M的坐标为或，

（3）如图，过点P作y轴的平行线，与x轴交于点N，与AD的延长线交于点Q，过D作DH⊥PQ，

当时，

故D点坐标为：（2，1），

设直线AD的解析式为y＝kx+n

将A（1，0），D（2，1）代入，解得 ，

∴直线AD的解析式为y＝x﹣1；

设P（x，﹣x2+4x﹣3），则Q（x，x﹣1），N（x，0），H（x，1）

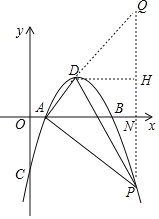
∴PQ＝（x﹣1）﹣（﹣x2+4x﹣3）＝x2﹣3x+2

∴S△ADP＝S△APQ﹣S△PQD＝＝＝＝＝，

∵S△ADP＝3

∴

即x2﹣3x﹣4＝0

解得：x1＝4，x2＝﹣1（舍）

将x＝4代入抛物线解析式，y＝﹣3

∴P（4，﹣3）．