题目内容
【题目】如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2 . 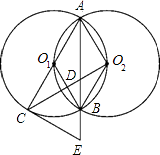
(1)求证:四边形AO1BO2是菱形;
(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E,连接CO2交AE于D,求证:CE=2O2D;
(3)在(2)的条件下,若△AO2D的面积为1,求△BO2D的面积.
【答案】
(1)证明:∵⊙O1与⊙O2是等圆,
∴AO1=O1B=BO2=O2A,
∴四边形AO1BO2是菱形;
(2)证明:∵四边形AO1BO2是菱形,
∴∠O1AB=∠O2AB,
∵CE是⊙O1的切线,AC是⊙O1的直径,
∴∠ACE=∠AO2C=90°,
∴△ACE∽△AO2D,
![]() ,
,
即CE=2DO2;
(3)解:∵四边形AO1BO2是菱形,
∴AC∥BO2
∴△ACD∽△BO2D,
∴ ![]() ,
,
∴AD=2BD,
∵ ![]() ,
,
∴ ![]() ,
,

【解析】(1)根据⊙O1与⊙O2是等圆,可得AO1=O1B=BO2=O2A,利用四条边都相等的四边形是菱形可判定出结论;(2)根据已知得出△ACE∽△AO2D,进而得出 ![]() ,即可得出答案;(3)首先证明△ACD∽△BO2D,得出
,即可得出答案;(3)首先证明△ACD∽△BO2D,得出 ![]() ,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
,AD=2BD,再利用等高不等底的三角形面积关系得出答案即可.
【考点精析】掌握菱形的判定方法和相交两圆的性质是解答本题的根本,需要知道任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;相交的两个圆的连心线垂直平分两圆的公共弦.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案【题目】老王的鱼塘里年初养了某种鱼2000条,到年底捕捞出售,为了估计鱼的总产量,从鱼塘里捕捞了三次,得到如下表的数据:
鱼的条数 | 平均每条鱼的质量 | |
第一次捕捞 | 10 | 1.7千克 |
第二次捕捞 | 25 | 1.8千克 |
第三次捕捞 | 15 | 2.0千克 |
若老王放养这种鱼的成活率是95%,则:
(1)鱼塘里这种鱼平均每条重约多少千克?
(2)鱼塘里这种鱼的总产量是多少千克?