题目内容
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).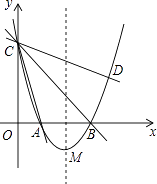
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数.
【答案】
(1)
解:将M(2,﹣1)、B(3,0)代入抛物线的解析式中,得:
![]() ,
,
解得 ![]() .
.
故抛物线的解析式:y=x2﹣4x+3.
(2)
解:由抛物线的解析式知:B(3,0)、C(0,3)、A(1,0);
则△OBC是等腰直角三角形,∠OBC=45°.
过B作BE⊥x轴,交直线CD于E(如下图),
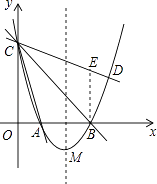
则∠EBC=∠ABC=45°;
由于直线CD和直线CA关于直线CB对称,所以点A、E关于直线BC对称,则BE=AB=2;
则E(3,2).
由于直线CD经过点C(0,3),可设该直线的解析式为y=kx+3,代入E(3,2)后,得:
3k+3=2,k=﹣ ![]()
故直线CD的解析式:y=﹣ ![]() x+3.
x+3.
(3)
解:设P(2,m),已知M(2,﹣1)、B(3,0)、C(0,3),则:
PM2=(2﹣2)2+(m+1)2=m2+2m+1,PB2=(3﹣2)2+(0﹣m)2=m2+1,PC2=(0﹣2)2+(3﹣m)2=m2﹣6m+13;
已知:PM2+PB2+PC2=35,则:m2+2m+1+m2+1+m2﹣6m+13=35,化简得:3m2﹣4m﹣20=0
解之得:m1=﹣2,m2= ![]() ;
;
则P1(2,﹣2)、P2(2, ![]() )
)
当点P坐标为(2, ![]() )时,由图可知,直线OP与抛物线必有两个交点;
)时,由图可知,直线OP与抛物线必有两个交点;
当点P坐标为(2,﹣2)时,直线OP:y=﹣x,联立抛物线的解析式有:
x2﹣4x+3=﹣x,即 x2﹣3x+3=0
△=(﹣3)2﹣4×3<0,
故该直线与抛物线没有交点;
综上,直线OP与抛物线有两个交点.
【解析】(1)抛物线的解析式中只有两个待定系数,将已知的两点坐标代入其中进行求解即可.(2)由C、B两点的坐标不难判断出OB=OC,即∠CBO=45°,那么若取BE⊥x轴交CD于E,结合“直线CD和直线CA关于直线CB对称”可得出A、E关于直线BC对称,结合点B的坐标以及AB的长即可得到点E的坐标,在明确C、E两点坐标的情况下,直线CD的解析式即可由待定系数法求得.(3)先设出点P的坐标,而M、B、C三点坐标已知,即可得到PM2、PB2、PC2的表达式,结合题干的已知条件即可求出点P的坐标,从而进一步判断出直线OP与抛物线的交点个数.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表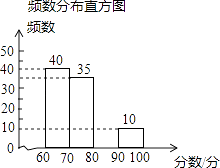
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.