��Ŀ����
����Ŀ����֪��������![]() ��������ԭ�㣬�ҵ�
��������ԭ�㣬�ҵ�![]() ʱ, y��x���������С.
ʱ, y��x���������С.
��1���������ߵĽ���ʽ��
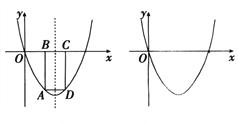
��2������ͼ�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB![]() x���ڵ�B, DC
x���ڵ�B, DC![]() x���ڵ�C.
x���ڵ�C.
�ٵ� BC=1ʱ��ֱ��д������ABCD���ܳ���
���趯��A������Ϊ��a, b��,������ABCD���ܳ�L��ʾΪa�ĺ�������д���Ա�����ȡֵ��Χ���ж��ܳ��Ƿ�������ֵ��������ڣ����������ֵ���������ʱ��A�����ꣻ��������ڣ���˵������.
���𰸡���1��![]() ����2����6 ����L=
����2����6 ����L= ����A��������
����A��������![]() ����
����![]() ����
����![]() ����
����![]() ����L�����ֵΪ
����L�����ֵΪ![]() ��
��
�������������������1��������֪�������߹���0��0�������Խ���0��0������y=x2+��2m��1��x+m2��1�������m��ֵ������x��0ʱ��y��x���������С����֪�Գ���һ����y����Ҳ࣬�����ó�m��ȡֵ��Χ��
��2������AD��x�ᣬ����A��D���������ߵĶԳ���Գƣ��Ӷ��ó�B�ĺ����꣬���������߽���ʽ�������B�������꣬�Ӷ��ó�AB�ij��ȣ�
����A��a��b������y=x2��3x������b=a2��3a�����öԳ��Կ����D������Ϊ��3��a��a2��3a��������AD=|3��2a|��Ȼ�����������������ۣ�0��a��![]() ʱ��
ʱ��![]() ��a��3ʱ���ֱ����L��a�Ĺ�ϵʽ�����ö��κ��������ʼ������L����ֵ��
��a��3ʱ���ֱ����L��a�Ĺ�ϵʽ�����ö��κ��������ʼ������L����ֵ��
����������⣺��1���ѣ�0��0������y=x2+��2m��1��x+m2��1����0=m2��1����m=��1������x��0ʱ��y��x���������С�����Գ���x=![]() ��0����m��
��0����m��![]() ����m=��1���������ߵĽ���ʽΪy=x2��3x��
����m=��1���������ߵĽ���ʽΪy=x2��3x��
��2���١�AD��x�ᣬ��A��D���������ߵĶԳ���Գƣ��������ߵĶԳ���Ϊx=![]() ��BC=1
��BC=1
����B�ĺ�����Ϊ1������x=1����y=x2��3x����y=��2����AB=2��������ABCD���ܳ�Ϊ��2��2+2��1=6��
����A��a��b������y=x2��3x����b=a2��3a����A��a��a2��3a������y=0����y=x2��3x����x=0��x=3����������֪��0��a��3����AB=3a��a2��������֪��A��D����x=![]() �Գƣ���D������Ϊ��3��a��a2��3a������AD=|3��a��a|=|3��2a|��������������ۣ�
�Գƣ���D������Ϊ��3��a��a2��3a������AD=|3��a��a|=|3��2a|��������������ۣ�
��0��a��![]() ʱ����AD=3��2a����L=2��AB+AD��=��2a2+2a+6=��2��a��
ʱ����AD=3��2a����L=2��AB+AD��=��2a2+2a+6=��2��a��![]() ��2+
��2+![]() ����a=
����a=![]() ʱ��L�����ֵΪ
ʱ��L�����ֵΪ![]() ����ʱA������Ϊ��
����ʱA������Ϊ��![]() ����
����![]() ����
����
��![]() ��a��3ʱ����AD=2a��3����L=2��AB+AD��=
��a��3ʱ����AD=2a��3����L=2��AB+AD��=![]() =��2��a��
=��2��a��![]() ��2+
��2+![]() ����a=
����a=![]() ʱ��L�����ֵΪ
ʱ��L�����ֵΪ![]() ����ʱA������Ϊ��
����ʱA������Ϊ��![]() ����
����![]() ����
����
����������L=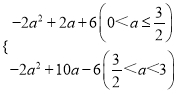 ����A��������
����A��������![]() ����
����![]() ����
����![]() ����
����![]() ����L�����ֵΪ
����L�����ֵΪ![]() ��
��

����Ŀ��ij��˾��Ƹ�˲ţ���ӦƸ�߷ֱ�����Ķ�������רҵ֪ʶ����������������ԣ�����������Ե÷ְ�3��5��2�ı���ȷ��ÿ�˵����ճɼ��������Ӽ�����ѡ����¼ȡһ�ˣ���֪���˵ĸ�����Ե÷����±�(��λ����)
�Ķ� | רҵ | ���� | |
�� | 93 | 86 | 73 |
�� | 95 | 81 | 79 |
����ͨ����صļ���˵��˭����¼�ã�
�������ѡ�߽���ӦƸ��Щ�����Ľ��飮



