Question

【题目】如图1，△ABC中，BE平分∠ABC交AC边于点E，过点E作DE∥BC交AB于点D，

（1）求证：△BDE为等腰三角形；

（2）若点D为AB中点，AB=6，求线段BC的长；

（3）在图2条件下，若∠BAC=60°，动点P从点B出发，以每秒1个单位的速度沿射线BE运动，请直接写出图3当△ABP为等腰三角形时t的值．

Answer 1

【答案】（1）详见解析；（2）BC=6；（3）当△ABP为等腰三角形时t的值为，6，.

【解析】

（1）由角平分线和平行线的性质可得到∠BDE=∠DEB，可证得结论；

（2）由条件可知BD=DE=DA=3，且DE为△ABC的中位线，可求得BC长；

（3）分BP=AP、BP=AB、AP=AB三种情况分别讨论求t的值即可．

（1）证明：∵BE平分∠ABC，

∴∠ABE=∠EBC，

∵DE∥BC，

∴∠DEB=∠EBC=∠ABE，

∴BD=ED，

∴△DBE为等腰三角形；

（2）∵点D为AB中点

∴AD=BD=ED=AB=3，

∵DE∥BC，

∴E为AC中点，

∴DE为△ABC的中位线，

∴BC=2DE=6；

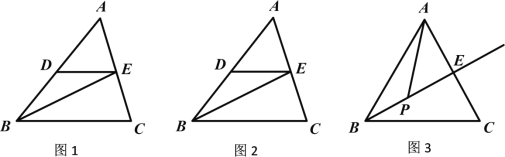
（3）在（2）的条件下可知DE=DA，且∠BAC=60°，∴△ADE为等边三角形，

∵BC=2DE=AB，

∴△ABC为等边三角形，

当BP=AP时，过点P作PE⊥AB，交AB于点E，则BF=AB=6，

在Rt△PBF中，∠PBF=∠ABC=30°，

∴BP=，即t=，

当BP=BA时，此时BP=6，即t=6，

当AB=AP时，此时，BP=2BE=，

即t=，

综上可知当△ABP为等腰三角形时t的值为，6，