Question

【题目】如图，在平面直角坐标系中，抛物线与直线分别交于轴、轴上的两点，设该抛物线与轴的另一个交点为点，顶点为点，联结交轴于点.

求该抛物线的表达式及点的坐标；

求的正切值；

如果点在轴上，且，求点的坐标.

Answer 1

【答案】（1）y=-x2+2x-3；（2）；（3）①；②

【解析】

（1）y=x-3，令y=0，则x=6，令x=0，则y=-3，求出则点B、C的坐标，将点B、C坐标代入抛物线y=-x2+bx+c，即可求解；

（2）求出点E（3，0），EH=EBsin∠OBC=，CE=3，则CH=，即可求解；

（3）分点F在y轴负半轴和在y轴正半轴两种情况，分别求解即可．

（1）y=x-3，令y=0，则x=6，令x=0，则y=-3，

则点B、C的坐标分别为（6，0）、（0，-3），则c=-3，

将点B坐标代入抛物线y=-x2+bx-3得：0=-×36-6b-3，

解得：b=2，

故抛物线的表达式为：y=-x2+2x-3，

令y=0，则x=6或-2，

即点A（2，0），

y=-x2+2x-3=- (x-4)2+1

则点D（4，1）；

（2）过点E作EH⊥BC交于点H，

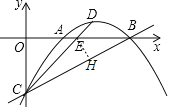
C、D的坐标分别为：（0，-3）、（4，1），

直线CD的表达式为：y=x-3，则点E（3，0），

tan∠OBC=，

则sin∠OBC=，

则EH=EBsin∠OBC=，

CE=3，则CH=，

则tan∠DCB=；

（3）点A、B、C、D、E的坐标分别为（2，0）、（6，0）、（0，-3）、（4，1）、（3，0），

则BC=3，

∵OE=OC，

∴∠AEC=45°，

tan∠DBE==，

故：∠DBE=∠OBC，

则∠FBC=∠DBA+∠DCB=∠AEC=45°，

①当点F在y轴负半轴时，

过点F作FG⊥BG交BC的延长线与点G，

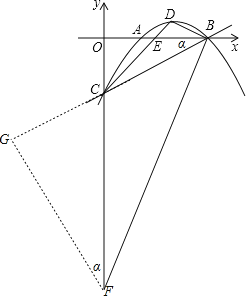
则∠GFC=∠OBC=α，

设：GF=2m，则CG=CGtanα=m，

∵∠CBF=45°，

∴BG=GF，

即：3+m=2m，解得：m=3，
CF==m=15，

故点F（0，-18）；

②当点F在y轴正半轴时，

同理可得：点F（0，2）；

故：点F坐标为（0，2）或（0，-18）．