题目内容
【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
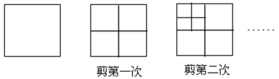
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.
【答案】(1)13;16;(2)an=3n+1;(3)见解析.
【解析】
观察数据可知,每剪一次便增加3个小正方形,按此规律可写出剪第4次和第5次所得到的小正方形的个数,并列出![]() 的表达式,由表达式分析是否能得到2018个小正方形即可.
的表达式,由表达式分析是否能得到2018个小正方形即可.
(1)观察表格数据可知剪第4次可得到13个小正方形,剪第5次可得到16个小正方形;
(2)由上述规律可得an=4+3×(n-1)=3n+1;
(3)当an=2018时,3n+1=2018,n=672.3333…,由于n不是一个整数,所以不能得到2018个小正方形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.

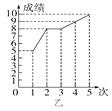
(1)请你根据图中的数据填写表格;
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | ||
乙 | 8 | 2.8 |
(2)从平均数和方差相结合看,谁的成绩好些?从发展趋势来看,谁的成绩好些?