��Ŀ����
����Ŀ��ijѧУΪ�˷ḻѧ�������������������������������Ŀ��A���滭�� B��������C����ģ D������ֲ��Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺ 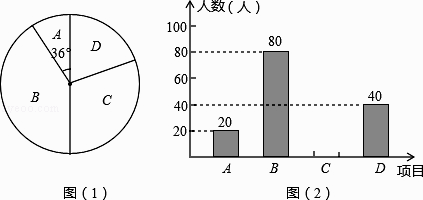
��1����α������ѧ�������ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ�ı�������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μӱ������������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
���𰸡�
��1��200
��2���⣺C��Ŀ��Ӧ����Ϊ��200��20��80��40=60���ˣ���
������ͼ��

��3���⣺����״ͼ�ã�

�߹���12�ֵȿ��ܵ������ǡ��ѡ�мס�����λͬѧ����2�֣�
��P��ѡ�мס��ң�= ![]() =
= ![]()
���������⣺��1����A����20�ˣ���ռ���ε�Բ�Ľ�Ϊ36�㣬 ����α������ѧ�����У�20�� ![]() =200���ˣ���
=200���ˣ���
�ʴ�Ϊ��200��
��1����A����20�ˣ���ռ���ε�Բ�Ľ�Ϊ36�㣬���������α������ѧ��������2���������C��Ŀ��Ӧ���������ɲ�ȫͳ��ͼ����3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ��ѡ�мס�����λͬѧ������������ø��ʹ�ʽ������ô𰸣�

����Ŀ����ͼ��ʾ����һ��������ֽƬ�����ĸ���Сһ����С�����Σ�Ȼ������һ��С�������ٰ�ͬ���ķ��������ĸ�С�����Σ��ٽ����е�һ��С�����μ����ĸ�С�����Σ����ѭ��������ȥ��
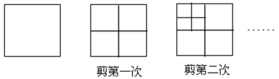
(1)����±���
���Ĵ��� | 1 | 2 | 3 | 4 | 5 | ... | n |
С�����εĸ��� | 4 | 7 | 10 | ... |
|
��2��![]() .���ú�n�Ĵ���ʽ��ʾ��
.���ú�n�Ĵ���ʽ��ʾ��
��3���������������ܷ�õ�2018��С�����Σ�����ܣ������n;�粻�ܣ���˵������.