题目内容
【题目】如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=﹣x2+bx+c经过原点O和点P,已知正方形ABCD的三个顶点为A(2,2),B(3,2),D(2,3).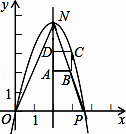
(参考公式:y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ![]() ,
, ![]() ).
).
(1)若当n=4时求c,b并写出抛物线对称轴及y的最大值;
(2)求证:抛物线的顶点在函数y=x2的图像上;
(3)若抛物线与直线AD交于点N,求n为何值时,△NPO的面积为1;
(4)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
【答案】
(1)
解:当n=4时,则P(4,0),
∵抛物线y=﹣x2+bx+c经过原点O和点P,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x=﹣(x﹣2)2+4,
∴抛物线对称轴为直线x=2,
∵﹣1<0,
∴当x=2时,y有最大值4
(2)
证明:把O、P的坐标代入抛物线解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+nx=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∴抛物线顶点坐标为( ![]() ,
, ![]() ),
),
在y=x2中,当x= ![]() 时,y=
时,y= ![]() ,
,
∴抛物线的顶点在函数y=x2的图像上
(3)
解:在y=﹣x2+nx中,当x=2时,y=2n﹣4,
∴N点坐标为(2,2n﹣4),
∴N到x轴的距离为|2n﹣4|=2|n﹣2|,
∵P(n,0),
∴OP=n,
∴S△NPO= ![]() n×2|n﹣2|=n|n﹣2|,
n×2|n﹣2|=n|n﹣2|,
当△NPO的面积为1时,则有n|n﹣2|=1,
当n=2时,N、P重合,不成立,
当n>2时,则n2﹣2n=1,解得n=1+ ![]() 或n=1﹣
或n=1﹣ ![]() (此时n小于2,舍去),
(此时n小于2,舍去),
当0<n<2时,则2n﹣n2=1,解得n1=n2=1,
综上可知当n的值为1+ ![]() 或1时,△NPO的面积为1
或1时,△NPO的面积为1
(4)
解:∵抛物线解析式为y=﹣x2+nx,
∴当过A(2,2)时,代入可得2=﹣4+2n,解得n=3,
同理当抛物线过B时可求得n= ![]() ,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n=
,当抛物线过点C时可求得n=4,当抛物线过点D时可求得n= ![]() ,
,
∴n的取值范围为3≤n≤4
【解析】(1)把原点和P点坐标代入抛物线解析式可求得b、c,则可求得抛物线解析式,化为顶点式可求得其对称轴和最大值;(2)用n可表示出抛物线的解析式,则可求得其顶点坐标,代入y=x2进行验证即可;(3)可用n表示出N点坐标,则可表示出N到x轴的距离和OP的长,可表示出△NPO的面积,可得到关于n的方程,可求得n的值;(4)分别把A、B、C、D的坐标代入抛物线解析式可求得n的值,则可求得n的取值范围.

【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
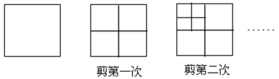
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.