题目内容
【题目】如图1,直线l交x轴于点C,交y轴于点D,与反比例函数y= ![]() (k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3
(k>0)的图像交于两点A、E,AG⊥x轴,垂足为点G,S△ADG=3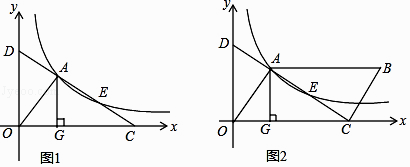
(1)k=;
(2)求证:AD=CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积.
【答案】
(1)6
(2)
证明:如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=kx+b,A(x1,y1),E(x2,y2).
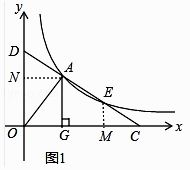
则有y1=kx1+b,y2=kx2+b,
∴y2﹣y1=k(x2﹣x1),
∴ ![]() ﹣
﹣ ![]() =k(x2﹣x1),
=k(x2﹣x1),
∴﹣kx1x2=3,
∴﹣kx1= ![]() ,
,
∴y2=﹣kx1,
∴EM=﹣kAN,
∵D(0,b),C(﹣ ![]() ,0),
,0),
∴tan∠DCO= ![]() =﹣k=
=﹣k= ![]() ,
,
∴EM=﹣kMC,
∴AN=CM,
∵AN∥CM,
∴∠DAN=∠ECM,
在△DAN和△ECM中,
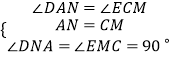 ,
,
∴△DAN≌△ECM,
∴AD=EC
(3)
解:如图2中,连接GD,GE.
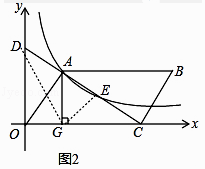
∵EA=EC,AD=EC,
∴AD=AE=EC,
∴S△ADG=S△AGE=S△GEC=3,
∵S△AOG=S△ADG=3,
∴S△AOC=3+3+3=9,
∴平行四边形ABCD的面积=2S△AOC=18
【解析】(1)解:设A(m,n),
∵ ![]() OGAG=3,
OGAG=3,
∴ ![]() mn=3,
mn=3,
∴mn=6,
∵点A在y= ![]() 上,
上,
∴k=mn=6.
所以答案是6.
【考点精析】掌握全等三角形的性质是解答本题的根本,需要知道全等三角形的对应边相等; 全等三角形的对应角相等.

【题目】小文同学每天乘从BRT(城市快速公交)上学,为了方便乘坐BRT,他用自己勤工俭学的钱买了80元的公交卡.如果他乘坐的次数用n表示,则记录他每次乘坐BRT后公交卡的余额(单位:元)如下表:
次数n | 余额(元) |
1 | 80-0.9 |
2 | 80-1.8 |
3 | 80-2.7 |
4 | 80-3.6 |
… | … |
(1)写出用乘坐BRT的次数n表示余额的式子为____________________;
(2)利用(1)中的式子,帮助小文同学算一算,他一个月乘坐BRT有84次,这80元的公交卡够不够用,若够用,能剩多少元?
(3)小文同学用80元的公交卡最多能乘坐BRT__________________次.
【题目】如图所示,将一张正方形纸片剪成四个大小一样的小正方形,然后将其中一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去。
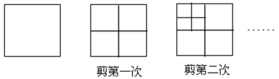
(1)完成下表:
剪的次数 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的个数 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代数式表示)
.(用含n的代数式表示)
(3)按上述方法,能否得到2018个小正方形?如果能,请求出n;如不能,请说明理由.