题目内容
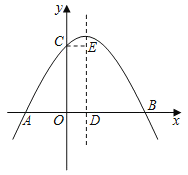
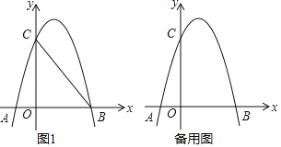
【题目】如图,抛物线y=mx2+nx﹣3(m≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点.
(1)求点C坐标及抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3;(2)![]() ;(3)点D的坐标为:(
;(3)点D的坐标为:(![]() ,﹣3﹣
,﹣3﹣![]() )、(﹣
)、(﹣![]() ,﹣3+
,﹣3+![]() )、(1,﹣3)
)、(1,﹣3)
【解析】
(1)设抛物线的表达式为:![]() ,解出a的值即可;
,解出a的值即可;
(2)设点P(x,x2+2x﹣3)、点M(x,﹣x),则PH=![]() PM=
PM=![]() ,将表达式配成顶点式即可得出答案;
,将表达式配成顶点式即可得出答案;
(3)分∠BCD=90°、∠CDB=90°两种情况,作出图形分别求解即可.
解:(1)∵抛物线与x轴交于A(﹣3,0),B(1,0)两点,
∴抛物线的表达式为:![]() ,
,
即﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3;
(2)过点P作PM∥y轴交直线EF于点M,
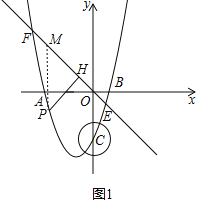
设点P(x,x2+2x﹣3)、点M(x,﹣x),
则PH=![]() PM=
PM=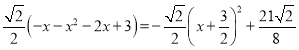 ,
,
当x=﹣![]() 时,PH的最大值为
时,PH的最大值为![]() ;
;
(3)①当∠BCD=90°时,如图2左侧图,
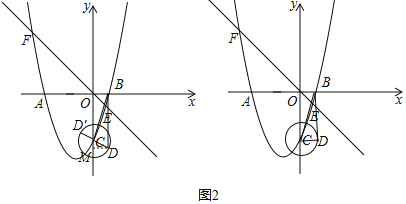
当点D在BC右侧时,
过点D作DM⊥y轴于点M,则CD=1,OB=1,OC=3,
tan∠BCO=![]() =tan∠CDM=tanα,则sinα=
=tan∠CDM=tanα,则sinα=![]() ,cosα=
,cosα=![]() ;
;
xD=CDcosα=![]() ,同理yD=﹣3﹣
,同理yD=﹣3﹣![]() ,
,
故点D(![]() ,﹣3﹣
,﹣3﹣![]() );
);
同理当点D(D′)在BC的左侧时,
同理可得:点D′(﹣![]() ,﹣3+
,﹣3+![]() );
);
②当∠CDB=90°时,
如右侧图,CD=OB=1,则点D(1,﹣3);
综上,点D的坐标为:(![]() ,﹣3﹣
,﹣3﹣![]() )、(﹣
)、(﹣![]() ,﹣3+
,﹣3+![]() )、(1,﹣3).
)、(1,﹣3).

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目