Question

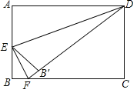
【题目】如图，在矩形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接ED，则DE的长度是_____，B′D的最小值是_____．

Answer 1

【答案】

【解析】

在直角△ADE中，根据勾股定理即可求出DE的长；连接DB′，如图1，则根据三角形的三边关系可得：，显然，当D、B′、E三点共线时，DB′最小，据此解答即可．

解：∵四边形ABCD是矩形，

∴∠A＝∠B＝90°，AD＝6，AB＝4，

∵E是AB边的中点，

∴AE＝BE＝＝2，

在直角△ADE中，根据勾股定理，得：DE＝．

连接DB′，如图1，则，

显然，当D、B′、E三点共线时，DB′最小，如图2，

∵，

∴．

故答案为：、．