Question

【题目】如图，把抛物线y= x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y= x2交于点Q，则图中阴影部分的面积为 ．

Answer 1

【答案】
【解析】解：过点P作PM⊥y轴于点M， ∵抛物线平移后经过原点O和点A（﹣6，0），
∴平移后的抛物线对称轴为x=﹣3，
得出二次函数解析式为：y= （x+3）2+h，
将（﹣6，0）代入得出：
0= （﹣6+3）2+h，
解得：h=﹣ ，
∴点P的坐标是（﹣3，﹣ ），
根据抛物线的对称性可知，阴影部分的面积等于矩形NPMO的面积，
∴S=|﹣3|×|﹣ |= ．
故答案为： ．

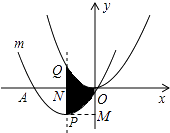
根据点O与点A的坐标求出平移后的抛物线的对称轴，然后求出点P的坐标，过点P作PM⊥y轴于点M，根据抛物线的对称性可知阴影部分的面积等于矩形NPMO的面积，然后求解即可．