题目内容
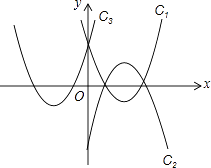
【题目】如图,抛物线L:y=﹣ ![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y= ![]() (k>0,x>0)于点P,且OAMP=12.
(k>0,x>0)于点P,且OAMP=12.
(1)求k的值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
【答案】
(1)
解:设P(x,y)则MP=y,
∵M为OA的中点,
∴OA=2x,
∵OAMP=12,
∴2xy=12,
∴xy=6,
∴k=6
(2)
解:当t=1,y=0时,0=﹣ ![]() (x﹣1)(x﹣1+4),解得x=1或x=﹣3,
(x﹣1)(x﹣1+4),解得x=1或x=﹣3,
∴A(1,0)、B(﹣3,0),
∴AB=4;
∴抛物线L的对称轴为直线x= ![]() =﹣1,
=﹣1,
∵OA=1,
∴MP为直线x= ![]() ,
,
∴直线MP与L对称轴之间的距离为 ![]()
(3)
解:在y=﹣ ![]() (x﹣t)(x﹣t+4)中,令y=0可得﹣
(x﹣t)(x﹣t+4)中,令y=0可得﹣ ![]() (x﹣t)(x﹣t+4)=0,解得x=t或x=t﹣4,
(x﹣t)(x﹣t+4)=0,解得x=t或x=t﹣4,
∴A(t,0),B(t﹣4,0),
∴抛物线L的对称轴为直线x= ![]() =t﹣2,
=t﹣2,
又∵MP为直线x= ![]() ,
,
∴当抛物线L的顶点在直线MP上或左侧时,即t﹣2≤ ![]() 时,解得t≤4,此时,顶点(t﹣2,2)为图象G最高点的坐标;
时,解得t≤4,此时,顶点(t﹣2,2)为图象G最高点的坐标;
当抛物线L的顶点在直线MP右侧时,即t﹣2> ![]() 时,解得t>4,此时时,交点直线MP与抛物线L的交点为(
时,解得t>4,此时时,交点直线MP与抛物线L的交点为( ![]() ,﹣
,﹣ ![]() t2+t),为图象G最高点的坐标
t2+t),为图象G最高点的坐标
【解析】(1)设P(x,y),则可表示出MP,由M为OA的中点,可求得OA,由条件可求得xy,则可求得k的值;(2)把t=1,代入抛物线解析式,令y=0可求得A、B两点的坐标,可求得AB的长,再求得抛物线的对称轴和直线MP的方程,可求得直线MP与对称轴之间的距离;(3)可用t表示出A、B两点的坐标,进一步可表示出直线MP的解析式,再根据顶点的位置可求得其最大值,可表示出G的坐标.
【考点精析】解答此题的关键在于理解反比例函数的概念的相关知识,掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数,以及对反比例函数的图象的理解,了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.

【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
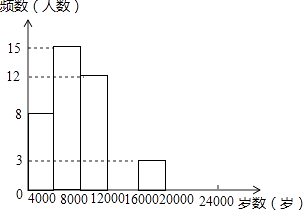
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.