题目内容
如图,在矩形ABCD中,AB=1,BC=3,点E为BC边上的动点(点E与点B、C不重合),设BE=x.
操作:在射线BC上取一点F,使得EF=BE,以点F为直角顶点、EF为边作等腰直角三角形EFG,设△EFG与矩形ABCD重叠部分的面积为S.
(1)求S与x的函数关系式,并写出自变量x的取值范围;
(2)S是否存在最大值?若存在,请直接写出最大值,若不存在,请说明理由.
(1)①当0<x≤1时, S= EF•FG=
EF•FG= x2(0<x≤1);
x2(0<x≤1);
②当1<x≤1.5时,S= (MN+EF)FN=x﹣
(MN+EF)FN=x﹣ (1<x≤1.5);
(1<x≤1.5);
③当1.5<x≤2时,S= (MD+EC)CD=﹣x+
(MD+EC)CD=﹣x+ (1.5<x≤2)
(1.5<x≤2)
④当2<x<3时, S= CE•CM=
CE•CM= x2﹣3x+
x2﹣3x+ (2<x<3);
(2<x<3);
(2)存在,其最大值为1.
解析试题分析:(1)本题要分情况进行讨论:
①当EF≤CD,即当0<x≤1时,重合部分是△EFG,两直角边的长均为x,由此可得出S,x的函数关系式.
②当CD<EF≤ BC,即当1<x≤1.5时,重合部分是个梯形,可用相似三角形求出梯形的上底的长,进而根据梯形的面积计算公式得出S,x的函数关系式.
BC,即当1<x≤1.5时,重合部分是个梯形,可用相似三角形求出梯形的上底的长,进而根据梯形的面积计算公式得出S,x的函数关系式.
③当EF> BC,但D在EG上或EG右侧,即当1.5<x≤2时,此时重合部分是个梯形,如果设EG与AD相交于点M,AD的延长线与FG相交于点N,可先在相似三角形GMN和GEF中求出MN的长,而后根据MD=MN﹣DN求出梯形的上底长,进而可按梯形的面积计算公式得出S,x的函数关系式.
BC,但D在EG上或EG右侧,即当1.5<x≤2时,此时重合部分是个梯形,如果设EG与AD相交于点M,AD的延长线与FG相交于点N,可先在相似三角形GMN和GEF中求出MN的长,而后根据MD=MN﹣DN求出梯形的上底长,进而可按梯形的面积计算公式得出S,x的函数关系式.
④当EF在D点右侧时,即当2<x<3时,重合部分是个三角形,先用x表示出两直角边的长,然后按①的方法进行求解即可.
(2)按上面分析的四种情况,分别进行求解,得出不同自变量的取值范围内S的最大值,然后进行比较即可得出S的最大值.
(1)①当0<x≤1时,FG=EF=x<1=AB(如图1),
∴S= EF•FG=
EF•FG= x2(0<x≤1);
x2(0<x≤1);
②当1<x≤1.5时,FG=EF=x>1=AB(如图2),
设EG与AD相交于点M,FG与AD相交于点N,
∵四边形ABCD是矩形
∴AD∥BC
∴∠GNM=∠GEF=45°,∠GNM=∠GFE=90°
∴∠MGN=45°
∴MN=GN=x﹣1
S= (MN+EF)FN=x﹣
(MN+EF)FN=x﹣ (1<x≤1.5);
(1<x≤1.5);
③当1.5<x≤2时,(如图3),设EG与AD相交于点M,AD的延长线与FG相交于点N,
∵四边形ABCD是矩形
∴AN∥BF
同理MN=GN=x﹣1
∵∠FNM=∠GFE=∠DCF=90°
∴四边形DCFN是矩形
DN=CF=BF﹣BC=2x﹣3,
MD=MN﹣DN=(x﹣1)﹣(2x﹣3)=2﹣x
S= (MD+EC)CD=﹣x+
(MD+EC)CD=﹣x+ (1.5<x≤2)
(1.5<x≤2)
④当2<x<3时,(如图4),
设EG与CD相交于点M
∵四边形ABCD是矩形,△EFG是等腰直角三角形,
∴∠MCE=90°,∠MEC=45°=∠CME
∴CM=CE=3﹣x
∴S= CE•CM=
CE•CM= x2﹣3x+
x2﹣3x+ (2<x<3);
(2<x<3);
(2)存在,其最大值为1.
考点:二次函数综合题.

 阅读快车系列答案
阅读快车系列答案 的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线. ,求点M的坐标.
,求点M的坐标.
 的图象与
的图象与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于
轴交于 点,已知点
点,已知点 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标; 是线段
是线段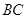 下方的抛物线上的一个动点,求
下方的抛物线上的一个动点,求 面积的最大值以及此时点
面积的最大值以及此时点
 的一元二次方程
的一元二次方程 有实数根,
有实数根, 为正整数.
为正整数. 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式;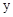 轴左侧的部分沿
轴左侧的部分沿 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出 的取值范围.
的取值范围.
 交坐标轴于A、B、D三点,过点D作
交坐标轴于A、B、D三点,过点D作 轴的平行线交抛物线于点C.直线l过点E(0,-
轴的平行线交抛物线于点C.直线l过点E(0,-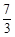 ),且平分梯形ABCD面积.
),且平分梯形ABCD面积.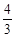 ,求点P的坐标.
,求点P的坐标.
 ,一抛物线过点A、B、 C.
,一抛物线过点A、B、 C.
 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点 是劣弧AO上一动点(
是劣弧AO上一动点( 不重合).抛物线y=-
不重合).抛物线y=- 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,
 交
交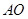 于点
于点 ,延长
,延长 ,使
,使 ,试探究当点
,试探究当点 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.