Question

如图，二次函数的图象与轴交于、两点，与轴交于点，已知点（－1，0），点C(0，－2)．
（1）求抛物线的函数解析式；
（2）试探究的外接圆的圆心位置，并求出圆心坐标；
（3）此抛物线上是否存在点P,使得以P、A、C、B为顶点的四边形为梯形.若存在，请写出所有符合条件的P点坐标；若不存在，请说明理由；
（4）若点是线段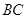下方的抛物线上的一个动点，求面积的最大值以及此时点的坐标．

Answer 1

(1) (2) 外接圆的圆心为AB的中点，且坐标为（，0）．(3) P₁(3,-2)、P₂(5,3)、P₃(-5,18) (4) 点M（2，﹣3），△MBC面积最大值是4.

解析试题分析：（1）把点 （－1，0），点C(0，－2)代入解析式，即可求出a、c的值，从而二次函数的解析式可求；
（2）首先根据抛物线的解析式确定A点坐标，然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置，由此确定圆心坐标．
（3）根据梯形的定义即可求出点P的坐标；
（4）△MBC的面积可由S△MBC=BC×h表示，若要它的面积最大，需要使h取最大值，即点M到直线BC的距离最大，若设一条平行于BC的直线，那么当该直线与抛物线有且只有一个交点时，该交点就是点M．
（1）将A（－1，0）、点C(0，－2)．代入
求得： 
（2）∵A（-1，0）、C（0，-2）；
∴OA=1，OC=2，OB=4，
即：OC2=OA•OB，又：OC⊥AB，
∴△OAC∽△OCB，得：∠OCA=∠OBC；
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°，
∴△ABC为直角三角形，AB为△ABC外接圆的直径；
外接圆的圆心为AB的中点，且坐标为（，0）．
（3）共三个P₁(3,-2)、P₂(5,3)、P₃(-5,18) 
（4）已求得：B（4，0）、C（0，-2），可得直线BC的解析式为：y=x-2；
设直线l∥BC，则该直线的解析式可表示为：y=x+b，
当直线l与抛物线只有一个交点时，可列方程：
x+b=x²-x-2，即：x²-2x-2-b=0，且△=0；
∴4-4×（-2-b）=0，即b=-4；
∴直线l：y=x-4．
所以点M即直线l和抛物线的唯一交点，有：
，
解得：
即 M（2，-3）．
过M点作MN⊥x轴于N，
S△BMC=S梯形OCMN+S△MNB-S△OCB=×2×（2+3）+×2×3-×2×4=4．
∴点M（2，﹣3），△MBC面积最大值是4.
考点：二次函数综合题．