Question

【题目】设二次函数y=-（x+1）（x-a）（a为正数）的图象与x轴交于A、B两点（A在B的左侧），与y轴交于C点．直线l过M（0，m）（0＜m＜2且m≠1）且与x轴平行，并与直线AC、BC分别相交于点D、E．二次函数y=-（x+1）（x-a）的图象关于直线l的对称图象与y轴交于点P．设直线PD与x轴交点为Q，则：

（1）求A、C两点的坐标；

（2）求AD的值（用含m的代数式表示）；

（3）是否存在实数m，使CDAQ=PQDE？若能，则求出相应的m的值；若不能，请说明理由．

Answer 1

【答案】（1）A（-1，0），C（0，2），（2）AD=；（3）当a＞1时，才存在实数m使得△PQA∽△CDE，从而有CDAQ=PQDE，此时m=；当0＜a≤1时，不存在实数m使得CDAQ=PQDE．

【解析】

（1）分别令x=0和y=0代入y=-（x+1）（x-a）中可求得A、C两点的坐标；

（2）如图1，根据待定系数法求直线AC的解析式，表示点D的坐标，利用勾股定理可得AD的长；

（3）根据∠PQA=∠PDE，和CDAQ=PQDE，可知：△PQA∽△CDE，由对称可知：△CDE≌△PDE，

△PQA∽△PDE，分两种情况进行讨论：

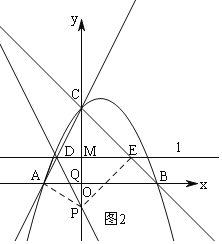
①当0＜m＜1时，点P在x轴下方，如图2，

②当1＜m＜2时，如图3，从相似入手，第一种情况不可能相似所以不成立，第二种情况根据相似列比例式可得m的值．

（1）当x=0时，y=-×1×（-a）=2，

∴点C的坐标为（0，2），

当y=0时，y=-（x+1）（x-a）=0，

∴x1=-1，x2=a，

∴点A坐标为（-1，0）；

（2）如图1，设直线AC的解析式为：y=kx+b，

把A（-1，0），C（0，2）代入得：，

解得：，

∴直线AC的解析式为：y=2x+2，

∵DM∥x轴，且M（0，m），

∴D（，m），

由勾股定理得：AD==；

（3）∵l∥x轴，

∵∠PQA=∠PDE，

当CDAQ=PQDE，即，

则△PQA∽△CDE，

由对称可知：△CDE≌△PDE，

∴△PQA∽△PDE，

分两种情况：

①当0＜m＜1时，点P在x轴下方，如图2，连接PA和PE，

此时∠PQA显然为钝角，

而∠PDE显然为锐角，故此时不能有△PQA∽△CDE．

②当1＜m＜2时，如图3，连接PA和PE，

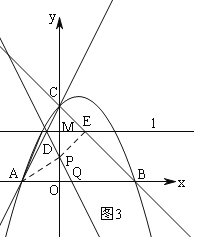
∵M（0，m），

∴OM=m，

∴CM=2-m，

∵CM=PM=2-m，

∴OP=OM-PM=m-（2-m）=2m-2，

∵△APQ∽△EPD，

∴，

∵D（，m），P（0，2m-2），

易得DP的解析式为：y=-2x+2m-2，

当y=0时，-2x+2m-2=0，

x=m-1，

∴Q（m-1，0），

∴AQ=1+m-1=m，

∵B（a，0），C（0，2），

易得直线BC的解析式为：y=-x+2，

当y=m时，-x+2=m，

x=，

∴E（，m），

∴DE==，

∴，

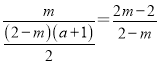∴m=，而此时1＜m＜2，

则应有1＜＜2，由此知a＞1．

综上所述，当a＞1时，才存在实数m使得△PQA∽△CDE，从而有CDAQ=PQDE，此时m=；当0＜a≤1时，不存在实数m使得CDAQ=PQDE．