题目内容
【题目】若∠A与∠B的两边分别垂直,请判断这两个角的数量关系.
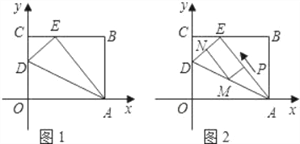
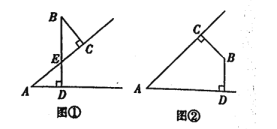
(1)如图①,∠A与∠B的数量关系是____,如图②,∠A与∠B的数量关系是____.
(2)请从图①或图②中选择一种情况说明理由。
【答案】(1)∠A=∠B(相等) ,∠A+∠B=180°(互补);(2)见解析.
【解析】
1)如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补;
(2)根据垂直的量相等的角都等于90°,对顶角相等,即可得出∠A=∠B,同样根据垂直的定义以及四边形的内角和等于360°,即可得出∠A+∠B=360°-90°-90°=180°.
(1)如图①,∠A=∠B(相等);如图②,∠A+∠B=180°(互补);
故答案为:相等,互补;
(2)选题图①,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
又∵∠A=180°-∠EDA-∠AED,∠B=180°-∠BCE-∠BEC,∠AED=∠BEC,
∴∠A=∠B.
选题图②,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
∵四边形的内角和等于360°,
∴∠A+∠B=360°-90°-90°=180°.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目