题目内容
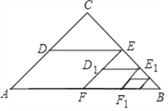
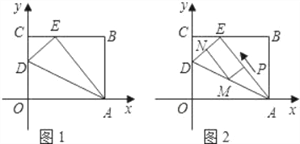
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
【答案】(1)D(0,2.5),E(2,4);(2)S =﹣0.5t2+2.5t,当t=2.5时,S矩形PMNE有最大值![]() ;(3)t=2.5或t=2
;(3)t=2.5或t=2![]() 时,以A,M,E为顶点的三角形为等腰三角形,M点的坐标为(2.5,1.25)或(5﹣2
时,以A,M,E为顶点的三角形为等腰三角形,M点的坐标为(2.5,1.25)或(5﹣2![]() ,
,![]() ).
).
【解析】试题分析:(1)根据折叠的性质可知:AE=OA,OD=DE,那么可在直角三角形ABE中,用勾股定理求出BE的长,进而可求出CE的长,也就得出了E点的坐标.在直角三角形CDE中,CE长已经求出,CD=OC-OD=4-OD,DE=OD,用勾股定理即可求出OD的长,也就求出了D点的坐标.
(2)很显然四边形PMNE是个矩形,可用时间t表示出AP,PE的长,然后根据相似三角形APM和AED求出PM的长,进而可根据矩形的面积公式得出S,t的函数关系式,根据函数的性质即可得出S的最大值及对应的t的值.
(3)本题要分两种情况进行讨论:
①ME=MA时,此时MP为三角形ADE的中位线,那么AP=![]() ,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.
,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.
②当MA=AE时,先在直角三角形OAD中求出斜边AD的长,然后根据相似三角形AMP和ADE来求出AP,MP的长,也就能求出t的值.根据折叠的性质,此时AF=AP,MF=MP,也就求出了M的坐标.
试题解析:
(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=5,AB=4.
BE=![]() =3.
=3.
∴CE=2.
∴E点坐标为(2,4).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD.
∴(4﹣OD)2+22=OD2.
解得:OD=2.5.
∴D点坐标为(0,2.5).
(2)如图②∵PM∥ED,
∴△APM∽△AED.
∴![]() ,
,
又知AP=t,ED=2.5,AE=5,PM=0.5t×2.5=0.5t,
又∵PE=5﹣t.
而显然四边形PMNE为矩形.
S矩形PMNE=PMPE=0.5t×(5﹣t)=﹣0.5t2+2.5t;
∴S四边形PMNE=﹣0.5(t﹣2.5)2+![]() ,
,
又∵0<2.5<5.
∴当t=2.5时,S矩形PMNE有最大值![]() .
.
(3)(i)若以AE为等腰三角形的底,则ME=MA(如图①)
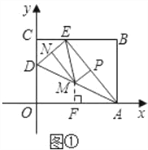
在Rt△AED中,ME=MA,
∵PM⊥AE,
∴P为AE的中点,
∴t=AP=0.5AE=2.5.
又∵PM∥ED,
∴M为AD的中点.
过点M作MF⊥OA,垂足为F,则MF是△OAD的中位线,
∴MF=0.5OD=1.25,OF=0.5OA=2.5,
∴当t=2.5时,(0<2.5<5),△AME为等腰三角形.
此时M点坐标为(2.5,1.25).
(ii)若以AE为等腰三角形的腰,则AM=AE=5(如图②)
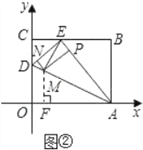
在Rt△AOD中,AD=![]() =
=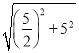 =
=![]() .
.
过点M作MF⊥OA,垂足为F.
∵PM∥ED,
∴△APM∽△AED.
∴![]() .
.
∴t=AP=![]() =
= ![]() =
=![]() ,
,
∴PM=![]() t=
t=![]() .
.
∴MF=MP=![]() ,OF=OA﹣AF=OA﹣AP=5﹣2
,OF=OA﹣AF=OA﹣AP=5﹣2![]() ,
,
∴当t=2![]() 时,(0<2
时,(0<2![]() <5),此时M点坐标为(5﹣2
<5),此时M点坐标为(5﹣2![]() ,
, ![]() ).
).
综合(i)(ii)可知,t=2.5或t=2![]() 时,以A,M,E为顶点的三角形为等腰三角形,
时,以A,M,E为顶点的三角形为等腰三角形,
相应M点的坐标为(2.5,1.25)或(5﹣2![]() ,
, ![]() ).
).
点睛:本题主要考查了矩形的性质,勾股定理,图形的翻折变换,相似三角形的判定和性质以及二次函数的综合应用等知识点,综合性较强.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案