题目内容
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4、…,△16的直角顶点的坐标为( )
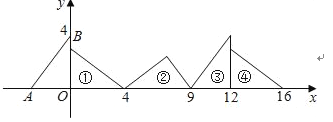
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
【答案】A
【解析】
根据题目提供的信息,可知旋转三次为一个循环,图中第三次和第四次的直角顶点的坐标相同,由①→③时直角顶点的坐标可以求出来,从而可以解答本题.
由题意可得,
△OAB旋转三次和原来的相对位置一样,点A(﹣3,0)、B(0,4),
∴OA=3,OB=4,∠BOA=90°,
∴AB=![]() =5,
=5,
∴旋转到第三次时的直角顶点的坐标为:(12,0),
16÷3=5…1
∴旋转第15次的直角顶点的坐标为:(60,0),
又∵旋转第16次直角顶点的坐标与第15次一样,
∴旋转第16次的直角顶点的坐标是(60,0),
故选A.

练习册系列答案
相关题目