题目内容
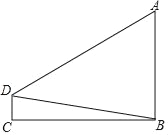
【题目】如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).

【答案】②③④.
【解析】
①如果OA=OD,则四边形AEDF是矩形,∠A=90°,不符合题意,所以①不正确;
②首先根据全等三角形的判定方法,判断出△AED≌△AFD,AE=AF,DE=DF;然后根据全等三角形的判定方法,判断出△AE0≌△AFO,即可判断出AD⊥EF;
③首先判断出当∠A=90°时,四边形AEDF的四个角都是直角,四边形AEDF是矩形,然后根据DE=DF,判断出四边形AEDF是正方形即可;
④根据△AED≌△AFD,判断出AE=AF,DE=DF,即可判断出AE+DF=AF+DE成立.
如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
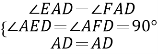
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,
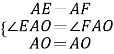 ,
,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故答案为:②③④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目