题目内容
【题目】在等腰△ABC中,AB=AC,∠BAC=45°,CD是△ABC的高,P是线段AC(不包括端点A,C)上一动点,以DP为一腰,D为直角顶点(D、P、E三点逆时针)作等腰直角△DPE,连接AE.

(1)如图1,点P在运动过程中,∠EAD=______,写出PC和AE的数量关系;
(2)如图2,连接BE.如果AB=4,CP=![]() ,求出此时BE的长.
,求出此时BE的长.
【答案】(1)45°;PC=AE,(2)![]() .
.
【解析】
(1)根据全等三角形的性质即可得到结论;
(2)根据等腰直角三角形的性质得到∠DEP=∠DPE=45°,DE=DP.根据全等三角形的性质得到AE=PC=![]() ∠EAD=∠ACD=45°,过点E作EF⊥AB于F.根据勾股定理即可得到结论.
∠EAD=∠ACD=45°,过点E作EF⊥AB于F.根据勾股定理即可得到结论.
解:(1)PC=AE,
∵∠EDP=∠ADC=90°,
∴∠ADE+∠ADP=∠ADP+∠CDP=90°,
∴∠ADE=∠CDP,
在△ADE与△CDP中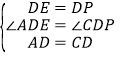 ,
,
∴△ADE≌△CDP(SAS),
∴∠EAD=∠PCD=45°,PC=AE;
故答案为:45°;
(2)如图,
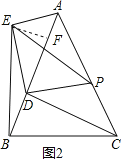
∵CD⊥AB,
∴∠ADC=90°.
∵∠BAC=45°,
∴AD=DC.
∵△DEP是等腰直角三角形,∠EDP=90°,
∴∠DEP=∠DPE=45°,DE=DP.
∵∠EDP=∠ADC=90°,
∴∠EDP-∠ADP=∠ADC-∠ADP.
∴∠EDA=∠PDC.
∴△EDA≌△PDC.(SAS),
∴AE=PC=![]() ∠EAD=∠ACD=45°,
∠EAD=∠ACD=45°,
过点E作EF⊥AB于F.
∴在Rt△AEF中,利用勾股定理,可得EF=AF=1,
∵AB=4,
∴BF=AB-AF=3.
∴BE=![]() =
=![]() .
.

练习册系列答案
相关题目