题目内容
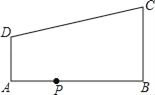
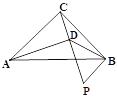
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,P为Rt△ABC外一点,且∠BPC=60°,过点A作AD⊥PC交PC于点D,连接BD,若∠PDB=45°,BD=![]() ,则PC= _____.
,则PC= _____.
【答案】![]()
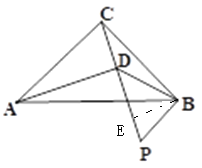
【解析】分析:过B作BE⊥PC于E,通过等腰直角三角形的性质和全等三角形的判定与性质,得到CD=BE,且△BED是等腰直角三角形,然后根据30°角的直角三角形求解即可.
详解:过B作BE⊥PC于E,
∵AD⊥PC,∠ACB=90°
∴∠CAD=∠BCE,
∴AD∥BE
∴∠DAB=∠EBA
∵AC=BC
∴△ACD≌△EBD
∴CD=BE,
∵∠PDB=45°
∠BCP+∠CBD=45°
∴∠EBA+∠DBA=∠CBD+∠DBA=45°
∴△BED是等腰直角三角形
∵BD=3![]()
∴BE=DE=3
即CD=3
又因∠P=60°
∴PE=![]()
∴PC=3+3+![]() =6+
=6+![]() .
.
故答案为:6+![]() .
.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目