题目内容
【题目】在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() .
.
(1)当![]() ,自变量
,自变量![]() 的取值范围是 (直接写出结果);
的取值范围是 (直接写出结果);
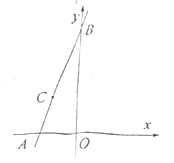
(2)点![]() 在直线
在直线![]() 上.
上.
①直接写出![]() 的值为 ;
的值为 ;
②过![]() 点作
点作![]() 交
交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)①1;②
;(2)①1;② ![]()
【解析】
(1)先利用直线y=3x+3确定A、B的解析式,然后利用一次函数的性质求解;
(2))①把C(-![]() ,n)代入y=3x+3可求出n的值;
,n)代入y=3x+3可求出n的值;
②利用两直线垂直,一次项系数互为负倒数可设直线CD的解析式为y=-![]() x+b,然后把C(-
x+b,然后把C(-![]() ,1)代入求出b即可.
,1)代入求出b即可.
解:(1)当y=0时,3x+3=0,解得x=-1,则A(-1,0),
当x=0时,y=3x+3=3,则B(0,3),
当0<y≤3,自变量x的取值范围是-1≤x<0;
(2)①把C(-![]() ,n)代入y=3x+3得3×(-
,n)代入y=3x+3得3×(-![]() )+3=n,解得n=1;
)+3=n,解得n=1;
②∵AB⊥CD,
∴设直线CD的解析式为y=-![]() x+b,
x+b,
把C(-![]() ,1)代入得-
,1)代入得-![]() ×(-
×(-![]() )+b=1,解得b=
)+b=1,解得b=![]() ,
,
∴直线CD的解析式为y=-![]() x+
x+![]() .
.

练习册系列答案
相关题目
【题目】六盘水市梅花山国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:cm)与滑行时间x(单位:s)之间的关系可以近似的用二次函数来表示.
滑行时间x/s | 0 | 1 | 2 | 3 | … |
滑行距离y/cm | 0 | 4 | 12 | 24 | … |
(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约800m,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向上平移5个单位,求平移后的函数表达式.