��Ŀ����
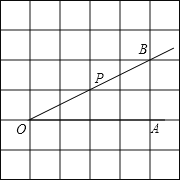
����Ŀ����ͼ��С����һ�ηŷ��ݻ��ijʱ�ε�ʾ��ͼ������A��ʱ�ķ����ߣ����������з����߽��Ƶؿ���ֱ�ߣ���ˮƽ�߹���30���ǣ��߶�AA1��ʾС������1.5�ף�
��1�������ݵ�ˮƽ����AC=18��ʱ�����ʱ������AD�ij��ȣ�
��2�������ӵ�A�ܶ�9![]() �����B��ʱ����������ˮƽ�߹���45���ǣ���ʱ���ݵ����E�������ݵ�ˮƽ�ƶ�����CF=10
�����B��ʱ����������ˮƽ�߹���45���ǣ���ʱ���ݵ����E�������ݵ�ˮƽ�ƶ�����CF=10![]() �ף���һ�����з����ߵij��ȱ��ֲ��䣬�����ԭ���ĸ߶�C1D��
�ף���һ�����з����ߵij��ȱ��ֲ��䣬�����ԭ���ĸ߶�C1D��
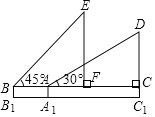
���𰸡���1��������AD�ij���Ϊ12![]() �ף���2������ԭ���ĸ߶�C1DΪ
�ף���2������ԭ���ĸ߶�C1DΪ![]() �ף�
�ף�
��������
��1����Rt��ACD�У���AD=![]() �ɵô𰸣�
�ɵô𰸣�
��2����AF=x�ף���BF=AB+AF=9![]() +x����Rt��BEF�����AD=BE=
+x����Rt��BEF�����AD=BE=![]() =18+
=18+![]() x����cos��CAD=
x����cos��CAD=![]() �ɽ�������x�ķ��̣���֮���x��ֵ�����ɵó�AD�ij����̶�����CD=ADsin��CAD���CD�Ӷ��ó��𰸣�
�ɽ�������x�ķ��̣���֮���x��ֵ�����ɵó�AD�ij����̶�����CD=ADsin��CAD���CD�Ӷ��ó��𰸣�
��1������Rt��ACD�У�cos��CAD=![]() ��AC=18����CAD=30�㣬
��AC=18����CAD=30�㣬
��AD=![]() =
=![]() ���ף���
���ף���
�𣺴�ʱ������AD�ij���Ϊ12![]() �ף�
�ף�
��2����AF=x�ף���BF=AB+AF=9![]() +x���ף���
+x���ף���
��Rt��BEF��BE=![]() =
=![]() =18+
=18+![]() x���ף���
x���ף���
������֪AD=BE=18+![]() x���ף���
x���ף���
��CF=10![]() ��
��
��AC=AF+CF=10![]() +x��
+x��
��cos��CAD=![]() �ɵ�
�ɵ�![]() ��
��
��ã�x=3![]() +2
+2![]() ��
��
��AD=18+![]() ����3
����3![]() +2
+2![]() ��=24+2
��=24+2![]() ��
��
��CD=ADsin��CAD=��24+3![]() ����
����![]() =
=![]() ��
��
��C1D=CD+C1C=![]() +
+![]() =
=![]() ��
��
�𣺷���ԭ���ĸ߶�C1DΪ![]() �ס�
�ס�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�