题目内容
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)解方程组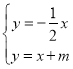 即可求出顶点
即可求出顶点![]() 的坐标;
的坐标;
(2)①根据二次函数的增减性列式求解即可;②当![]() 时,抛物线为
时,抛物线为![]() ,函数的最小值为
,函数的最小值为![]() ,所以可得
,所以可得![]() ,解之可求出
,解之可求出![]() 的取值范围;
的取值范围;
(3)联立两个关系式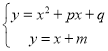 ,可得
,可得![]() ,然后根据一元二次方程根的判别式解答即可.
,然后根据一元二次方程根的判别式解答即可.
(1)由题意得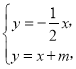 ,解得
,解得 ,
,
![]() .
.
(2)①根据题意得![]() ,解得
,解得![]() ,
,
![]() 的取值范围为
的取值范围为![]() .
.
②当![]() 时,顶点为
时,顶点为![]() ,
,
![]() 抛物线为
抛物线为![]() ,函数的最小值为
,函数的最小值为![]() ,
,
![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,
,
![]() ,
,
解得![]() .
.
(3)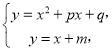 ,
,
得![]() ,
,
![]() ,
,
![]() ,
,
![]() 抛物线的顶点坐标既可以表示为
抛物线的顶点坐标既可以表示为![]() ,又可以表示为
,又可以表示为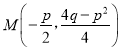 .
.
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 无论
无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?