Question

如图，已知反比例函数y=

m

x

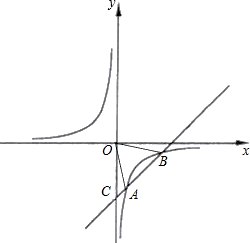的图象经过点A（1，-3），一次函数y=kx+b的图象经过点A与点C（0，-4），且与反比例函数的图象相交于另一点B（3，n）．
（1）试确定这两个函数的解析式；
（2）求△AOB的面积；
（3）根据图形直接写出反比例函数值大于一次函数值时自变量的取值范围．

Answer 1

分析：（1）根据A的坐标求反比例函数解析式，从而可求出B点坐标；根据A、C坐标求一次函数解析式；
（2）S_△AOB=S_△COB-S_△AOC；
（3）看在哪些区间反比例函数的图象在一次函数图象的上方．

解答：解：（1）∵y=

m

x

的图象经过点A（1，-3）
∴-3=

m

1

即m=-3
∴反比例函数解析式为：y=-

3

x

（2分）
又∵B(3，n)在y=-

3

x

上
∴n=-

3

b

=-1，即：B点坐标为（3，-1）
将A（1，-3）、B（3，-1）代入y=kx+b得：

k+b=-3 3k+b=-1

解得：

k=1 b=-4

．
∴一次函数解析式为：y=x-4；（5分）

（2）S_△AOB=S_△COB-S_△COA
=

1

2

•OC•|xB|-

1

2

•OC•|xA|
=

1

2

×4×3-

1

2

×4×1
=4；（8分）

（3）由图象可知：当x＜0或1＜x＜3时，反比例函数值大于一次函数值．（10分）

点评：根据函数图象解不等式时需从交点看起，图象在上方的函数值大．