题目内容
【题目】如图,在平面直角坐标系xOy中,抛物线与x轴相交于点A(-2,0)、B(4,0),与y轴交于点C(0,-4),BC与抛物线的对称轴相交于点D.
(1)求该抛物线的表达式,并直接写出点D的坐标;
(2)过点A作AE⊥AC交抛物线于点E,求点E的坐标;
(3)在(2)的条件下,点F在射线AE上,若△ADF∽△ABC,求点F 的坐标.

【答案】(1)![]() ,D(1,-3);(2)
,D(1,-3);(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】分析:(1)设抛物线的解析式为y=a(x+2)(x-4),将C(0,-4)代入求解即可;记抛物线的对称轴与x轴交点坐标为F,先求得抛物线的对称轴,则可得到FB的长,然后再证明△BFD为等腰直角三角形,从而可得到FD=FB=3,故此可得到点D的坐标;(2)过点E作EH⊥AB,垂为H.先证tan∠EAH=tan∠ACO=![]() ,设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;(3)记AE与抛物线的对称轴的交点为F,记对称轴与x轴的交点为G.由相似三角形的性质可得到∠ADF=∠ABC=45°,然后再证明∠ADF=45°,然后证明△AFG∽△AEH,最后,依据相似三角形的性质可求得FG的.
,设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;(3)记AE与抛物线的对称轴的交点为F,记对称轴与x轴的交点为G.由相似三角形的性质可得到∠ADF=∠ABC=45°,然后再证明∠ADF=45°,然后证明△AFG∽△AEH,最后,依据相似三角形的性质可求得FG的.
本题解析:解:设抛物线的解析式为y=a(x+2)(x-4),C(0,-4)代入得:-8a= -4,解:a=![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x-x-4.
x-x-4.
如下图所示:记抛物线的对称轴与x轴交点坐标为F.
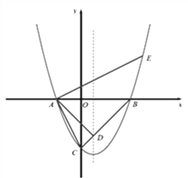
∵抛物线的对称轴为x=![]() =1, ∴BF=OB-OF=3, ∵BO=OC=4, ∠BOC=90°, ∴∠OBC=45. ∴△BFD为等腰直角三角形,∴FD=FB=3,∴D(1,-3)
=1, ∴BF=OB-OF=3, ∵BO=OC=4, ∠BOC=90°, ∴∠OBC=45. ∴△BFD为等腰直角三角形,∴FD=FB=3,∴D(1,-3)
(2)如下图:过点E作EH⊥AB,垂为H,
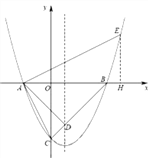
∵∠EAB+∠BAC=90°, ∠BAC+∠ACO=90°, ∴∠EAH=∠ACO, ∴tan∠EAH=tan∠ACO=![]() ,设EH=t,则AH=2t, ∴点E的坐标为(-2+2t,t),将(-2+2t,t)代入抛物线的解析式为:
,设EH=t,则AH=2t, ∴点E的坐标为(-2+2t,t),将(-2+2t,t)代入抛物线的解析式为: ![]() (-2+2t)-(-2+2t)-4=t,解得:t=
(-2+2t)-(-2+2t)-4=t,解得:t=![]() 或t=0(舍去),
或t=0(舍去),
∴E(5, ![]() ).
).
(3)如下图所示:
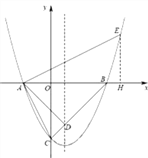
∵△ADF∽△ABC, ∴∠ADF=∠ABC=45°,由(2)知∠BDF=45°, ∵点A与点B关于DF对称,∴∠ADF=∠ABC, ∴点F在抛物线的对称轴上,∵FG∥EH, ∴△AFG∽△AEH. ∴![]() ,即
,即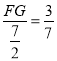 ,解得:FG=
,解得:FG=![]() ,∴F(1,
,∴F(1,![]() ).
).

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量![]() (万件)是销售单价
(万件)是销售单价![]() (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润![]() (万元)关于销售单价
(万元)关于销售单价![]() (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价![]() 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价![]() 的范围).
的范围).