题目内容
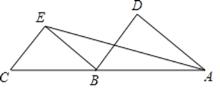
【题目】如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．
（1）求证：AD⊥BF；
（2）若BF=BC，求∠ADC的度数．
【答案】（1）证明见解析；（2）150°
【解析】试题分析：（1）连结DB、DF．根据菱形四边相等得出AB=AD=FA，再利用SAS证明△BAD≌△FAD，得出DB=DF，那么D在线段BF的垂直平分线上，又AB=AF，即A在线段BF的垂直平分线上，进而证明AD⊥BF；
（2）设AD⊥BF于H，作DG⊥BC于G，证明DG=
CD．在直角△CDG中得出∠C=30°，再根据平行线的性质即可求出∠ADC=180°﹣∠C=150°．
（1）证明：如图，连结DB、DF．
∵四边形ABCD，ADEF都是菱形，∴AB=BC=CD=DA，AD=DE=EF=FA．
在△BAD与△FAD中，∵AB=AF，∠BAD=∠FAD，AD=AD，∴△BAD≌△FAD，∴DB=DF，∴D在线段BF的垂直平分线上，∵AB=AF，∴A在线段BF的垂直平分线上，∴AD是线段BF的垂直平分线，∴AD⊥BF；
（2）如图，设AD⊥BF于H，作DG⊥BC于G，则四边形BGDH是矩形，∴DG=BH=
BF．∵BF=BC，BC=CD，∴DG=
CD．在直角△CDG中，∵∠CGD=90°，DG=
CD，∴∠C=30°，∵BC∥AD，∴∠ADC=180°﹣∠C=150°．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
